
영화 ‘기생충’이 25일(현지 시간) 제72회 칸 국제영화제에서 심사위원 만장일치로 황금종려상을 받았다는 소식이 전해졌습니다. 서영은 엄마가 뉴스에 놀라는 모습에 함께 이야기를 나눕니다.
서영: 한국 영화가 외국 영화보다 더 재미있다 보니, 세계에서도 주목하고 가치를 인정하는군요.
엄마: 영화 이야기가 나와서 말인데 영화에서 수학을 재미있게 다룬 작품도 많단다.
엄마: 이 기회에 재미난 수학 요소를 가진 영화를 몇 편 찾아서 보는 것도 재미있겠지?
○ 생사를 가르는 수학 문제
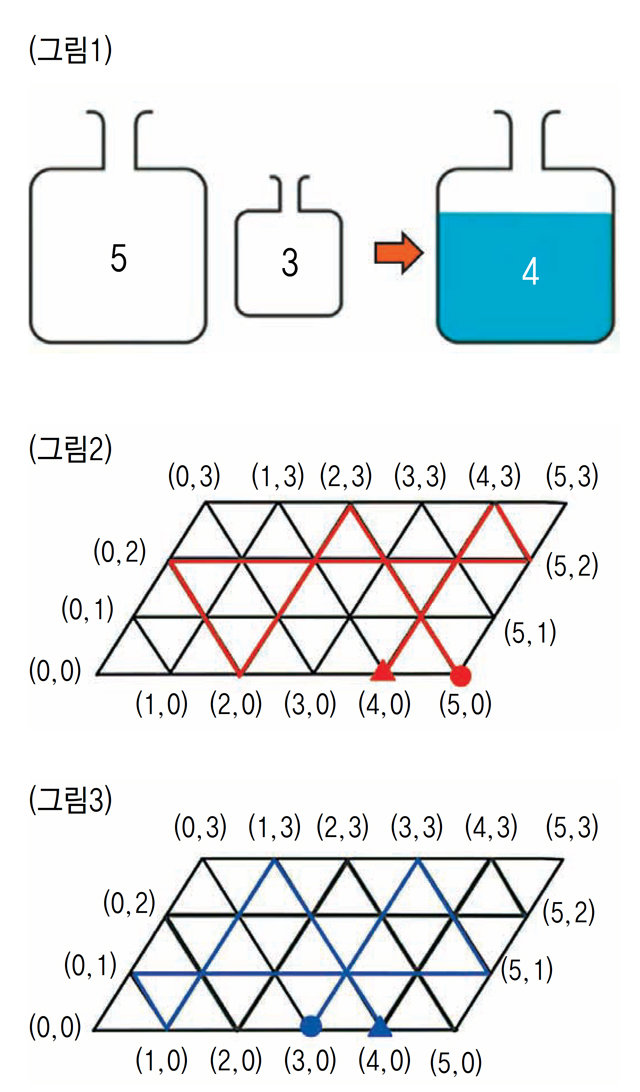
여러분이라면 어떻게 해결할 건가요? 두 물병의 물의 양을 순서대로 나타내 보면 다음과 같은 순서로 해결됩니다.
(5, 0)→(2, 3)→(2, 0)→(0, 2)→(5, 2)→(4, 3)→(4, 0)
여기 흥미로운 해결 방법이 있습니다. 평행사변형 당구대가 그것입니다. 당구대는 ‘그림 2’처럼 물통의 양과 같이 5칸×3칸으로 구성하되 정삼각형으로 이루어진 모눈을 사용합니다. 또 좌표를 도입해 왼쪽 아래 모퉁이가 (0,0), 오른쪽 위의 모퉁이가 (5,3)이 되도록 가장자리에 그림과 같이 좌표를 표시합니다. 이제 (5,0)에서 출발해 모눈을 따라 당구대 가장자리를 향해 쳐 보낸다고 할 때 당구대 가장자리에서 연이어 튕김에 따라 그때 점들의 좌표를 기록하면 앞서 구한 방법과 같음을 알 수 있습니다. 각각의 좌표는 각 통에 물을 채우거나 비우는 것 또는 옮기는 행위에 해당됩니다.
(4, 0)에서 모눈을 따라 계속 공을 튕겨 (0, 3)으로 끝내면 역으로 3L 물병을 가득 채워 시작하는 다음의 방법으로 4L를 얻을 수 있습니다.(그림 3)
가장자리의 좌표에 주목해 두 물통으로 0∼8L까지 채우기는 매우 쉽게 계획할 수 있습니다. 또 다른 양의 물통을 가지고도 칸을 조정한 모눈을 활용해 필요한 양을 구하는 경우를 계획할 수 있습니다.
○ 안전한 방의 비밀은 소수
영화 ‘큐브’(1997년)는 사람들이 큐브라는 밀실에서 깨어나면서 탈출구를 찾는 영화입니다. 각 정육면체 방에는 특별한 숫자 라벨이 암호화돼 있고, 일정 시간이 지난 후 6개의 정사각형 문이 있으며, 문을 통해 연결된 방 중 하나만이 안전하게 출구로 연결돼 있습니다. 등장인물들이 탈출을 시도하려다 일행 한 명을 잃고 나서야 한 방과 그 옆방에서 다음과 같은 숫자 라벨을 발견합니다. 다음 중 안전한 방은 어느 방일까요?
주인공은 이 숫자를 열심히 보다 소수가 첫 번째 열쇠임을 알아냅니다. 즉 이 수 가운데 소수가 하나라도 있으면 그 방에는 덫이 있고, 하나도 없으면 안전하다는 것인데요. ‘소수’는 1보다 큰 자연수 가운데 1과 자기 자신만을 약수로 가지는 수를 뜻합니다. 예를 들어 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31과 같은 수입니다. 세 자리 자연수가 소수인지 아닌지는 어떻게 알아낼까요?
세 자리 자연수 중 가장 큰 수는 999로 32×32=1024보다는 작고 31×32=992보다는 큰 수입니다. 따라서 세 자리 자연수가 소수인지는 31까지의 위의 소수 중 해당 수가 나누어떨어지는지를 빨리 확인해 봄으로써 알 수 있습니다. 더 이상 나눠지는 수가 없으면 소수인 것이지요. 두 방 중 하나를 골랐나요? 연습으로 137은 소수일까요? 645는 5의 배수, 372는 2의 배수, 649는 11의 배수입니다. 즉 어느 하나도 소수가 아니니까 안전한 방입니다.
○ 논리적 관계로 해 찾기
영화 ‘페르마의 밀실’(2007년)은 수학자들이 미지의 인물의 파티에 초대받아 수학 문제를 풀어달라는 요청을 받는 데서 시작됩니다. 그러나 이것은 곧 함정임이 드러나고 7개의 퍼즐을 제시해 지정된 시간 안에 퍼즐을 풀지 못하면 방이 줄어들게 됩니다. 퍼즐 문제는 다음과 같습니다.
한 학생이 교수에게 묻는다. “자제분 셋의 나이가 어떻게 됩니까?” 교수는 이렇게 대답한다. “곱하면 36이 되고, 더하면 우리 집 번지수와 같습니다.”
“선생님 번지수는 알고 있지만, 그것만 가지고는 모르겠는데요.” 교수는 이렇게 또 대답한다. “그렇겠군요. 큰애는 위층에 삽니다.”
세 자녀의 나이를 찾을 수 있을까요? 세 자녀의 나이를 곱한 값이 36이라 했으니 가능한 해를 나열해 보면 다음과 같습니다.
(1, 1, 36) (1, 2, 18) (1, 3, 12) (1, 4, 9) (1, 6, 6) (2, 2, 9) (2, 3, 6) (3, 3, 4)
그런데 학생이 번지수는 알고 있지만 그것만으로는 알 수 없다고 했으므로 합이 동일한 세 수가 있다는 뜻입니다. (1, 6, 6)과 (2, 2, 9)는 둘 다 합이 13입니다. 그런데 마지막 말에서 큰아이는 한 명이라는 것을 알 수 있고, 따라서 세 자녀의 나이는 (2, 2, 9)라는 것을 알아낼 수 있습니다.
영화 속에 숨겨둔 수학적 요소를 찾으면 색다른 재미를 느낄 수 있습니다. 여러분 중 누군가가 수학 요소들을 음악이나 영화 등 대중문화에 녹여 창의성과 재미 그리고 감동으로 영예로운 상을 받는 날을 기대해 봅니다.
박지현 반포고 교사
신문과 놀자!(초중고생을 위한 NIE) >
구독
이런 구독물도 추천합니다!
-

패션 NOW
구독 1
-

광화문에서
구독
-

사설
구독 806
-
- 좋아요
- 0개
-
- 슬퍼요
- 0개
-
- 화나요
- 0개
![[신문과 놀자!/함께 떠나요! 세계지리 여행]물 자원 둘러싼 국제 갈등… 국가 간 수심 깊어진다](https://dimg.donga.com/a/180/101/95/2/wps/NEWS/IMAGE/2025/03/10/131178429.5.jpg)



댓글 0