‘베다 수학’ 기계 같은 계산속도… IT 강국 인도의 비밀

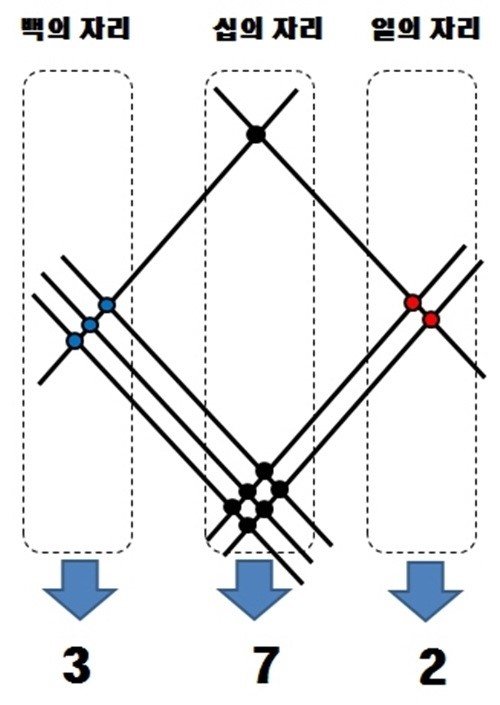
고대 인도의 ‘베다 수학’에 대한 네티즌들의 관심이 지난 15일에 이어 지금까지 상승하고 있다. ‘베다 수학’은 현대 수학의 기원이라는 평가가 지배적이다.

인도 베다 수학은 고대 인도에서 형성돼 발전해 온 수학 체계로 고대부터 입으로만 전해져 온 브라만의 힌두교 경전인 ‘베다(Veda)’에 기반해 베다 수학으로 불리며, ‘베다’에 나오는 계산법과 수학 지식들이 발전해 오늘날의 수학에 큰 영향을 끼쳤다.

인도 베다 수학은 특유의 사칙연산법으로 더 유명하며 곱셈 뺄셈 방정식 등도 베다 수학을 이용하면 쉽다.

덧셈의 경우 ‘75+38=113’ 을 예로들면 75은 70+5로, 38은 30+8로 분리하고, 이중 일의자리 덧셈 5+8의 답 13은 다시 10+3으로 파악한다. 이에 따라 75+38=70+30+10+3=113 공식이 성립돼 편하게 계산하면 된다.

뺄셈법은 경우에 따라 두 가지 방법이다. 보통은 10의 배수를 이용하는데, 빼는 수에 일정 숫자를 더해 10의 배수로 거듭난다. ‘75-38=37’ 이 그 예다. 38에 2를 더해 10의 배수인 40으로 만들어 75-40=35을 계산을 이끈다. 여기에 다시 38을 40으로 만든 숫자 2를 더하면 결과가 도출된다.

이런 인도 베다 수학은 100이나 1000 같은 숫자에서 뺄셈을 할 경우에 쉽다. 예를 들어 1000-137=863을 계산하려면 먼저 137중 1과 3을 본다. 9에서 1과 3을 뺀 숫자 8과 6이 각각 백의자리와 십의자리가 된다. 일의자리는 10에서 137 중 숫자 7을 뺀 3으로 결과가 도출된다.

인도 베다 수학의 곱셈법은 방법이 매우 다양하게 사용할 수 있다. 핵심은 덧셈 방식에서 파생된 것이다. 예를 들어 17x13=221을 계산한다면 먼저 각 숫자 17과 13을 10+7, 10+3으로 구별한다. 이중 십의자리수끼리 곱해 10x10=100으로 답을 구할 수 있다. 이어 십의자리와 일의자리를 각각 교차해 10x7=70, 10x3=30을 낸다. 그리고 일의자리끼리 곱해 7x3=21을 생성한다. 마지막으로 구한 값을 모두 더해 최종값인 100+70+30+21=221이 답이 나온다.

동아닷컴 도깨비뉴스 페이스북 http://www.facebook.com/DKBnews