[황규인의 잡학사전] 北核, 히로시마 원폭 ○배 위력…어떻게 계산?

1946년 7월 1일 서태평양 비키니 환초(atoll)에서 실시한 세계 최초 원자 폭탄 투하 공개 핵실험 장면. 동아일보DB.

‘핵실험’을 하면 왜 ‘지진’이 날까요?

정답은 ‘지하에서 폭탄을 터뜨려서’입니다.

1945년 처음 핵무기를 만든 뒤 70년 넘게 흐르는 동안 전 세계에서 이 무기가 제대로 작동하는지 시험한 건 2000번 정도 됩니다. 이 중 4분의 3 정도가 지하 핵실험이었습니다.

핵무기도 기본적으로 ‘폭탄’입니다. 폭탄은 폭발할 때 바깥으로 튀어나가려는 에너지로 적에게 피해를 입히는 무기. 땅속에서 이 에너지가 뻗어나가면서 땅이 흔들리게 됩니다.

그래서 핵실험을 하면 순간적으로 ‘인공 지진’이 일어나고 다른 지진과 마찬가지로 규모를 측정할 수 있게 되죠. 북한이 3일 강행한 6차 핵실험 규모는 기상청 발표 기준으로 5.7이었습니다.
●리히터(릭터) 규모란 무엇인가

그러면 여기서 규모는 뭘까요? 학창시절 과학 시간에 공부를 열심히 하신 분이라면 이 순간 ‘리히터 규모’라는 낱말을 떠올리실 겁니다.

리히터 규모는 찰스 릭터 미국 스탠퍼드대 교수(1900~85·아래 사진)가 1935년 처음 고안했습니다. 조상이 독일계라 예전에는 ‘Richter’라는 성(姓)을 ‘리히터’라고 적었죠. 그래서 많은 분에게 여전히 리히터 규모라는 표현이 익숙하지만 릭터 규모라는 말도 씁니다.

리히터 규모는 진앙(震央)에서 100㎞ 떨어진 지점에서 측정합니다. 이때 지진계가 진폭 1mm인 파형을 그리면 리히터 규모 3입니다. 딱 100㎞ 떨어진 지점에 반드시 지진계가 있으리라는 보장은 없기에 여러 곳에서 자료를 측정해 보정 과정을 거칩니다. 이런 이유로 발표 기관마다 규모가 다르거나 똑같은 지진에 대해 나중에 규모가 바뀌기도 합니다. 또 파형과 거리에 따라 다른 공식을 쓰는 것도 발표 기관마다 리히터 규모를 다르게 발표하는 이유이기도 합니다.

동아일보DB

그런데 왜 1mm일 때 규모가 1이 아니라 3일까요? 그건 지진계가 1000분의 1mm인 미크론을 단위로 쓰기 때문입니다. 그러면 1mm는 1000미크론이 되겠죠? 눈치가 빠른 분은 이미 아시겠지만 리히터 규모는 상용로그값입니다. 수학 시간에 배운 것처럼 상용로그는 밑을 10으로 하는 로그값입니다. 10^3=1000이기 때문에 1mm일 때 규모가 3이 되는 겁니다.

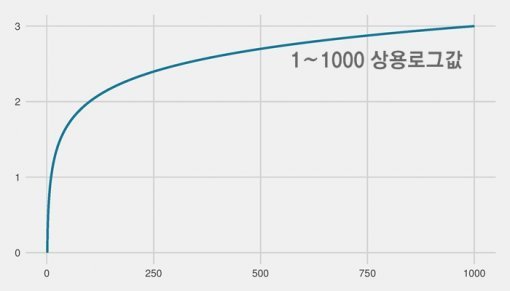
그러면 리히터 규모가 1이 커지면 진폭은 얼마나 커질까요? 이걸 알아보려면 상용로그값이 1이 나오는 숫자를 찾아야겠죠? 그럼 10이 답이니까 10배가 정답입니다. 2 차이가 나면? 네, 이번에는 100배가 정답입니다. 수학 시간에 로그 같을 걸 배워서 뭐 하나 싶어도 다 쓸 데가 있던 겁니다.

이렇게 지진계가 흔들리면 에너지가 나오겠죠? 이 에너지는 진폭 차이의 1.5제곱만큼 커집니다. 그래서 리히터 규모가 1 차이가 나면 언론에서는 보통 32배 차이가 난다고 표현합니다. 10의 1.5승이 31.6227766이거든요. 2 차이가 나면? 1000배 차이입니다. ((10^1.5)^2)=1000이니까요. 물론 수학 문제를 푸실 게 아니면 이걸 기억하고 계실 필요는 없습니다. 그냥 그렇다고 이해하고 넘어가시면 그만입니다.
●히로시마 몇 배는 어떻게 계산할까

이렇게 공식으로 계산하기 때문에 핵실험 파괴력을 다른 폭탄하고 비교하는 것도 가능합니다. 주로 1945년 일본 히로시마에 떨어진 첫 번째 원자폭탄 ‘리틀보이’와 비교하는 게 일반적입니다. 예를 들어 이번 북한 핵실험은 히로시마 원자폭탄 3~4배라는 평가를 어렵지 않게 찾아볼 수 있습니다. 이건 어떻게 하는 걸까요?

미 국방부 홈페이지

유용규 기상청 기상화산감시과장은 “‘규모 = 0.84 × TNT양(kt) 로그값 + 4.28’로 계산할 수 있다”며 “이를 역산하면 규모 5.7은 TNT 50kt에 해당한다”고 설명했습니다. 여기서 kt는 ‘킬로톤’이라고 읽죠. 1000t이 1kt입니다.

히로시마에 떨어진 리틀보이는 보통 TNT 15kt로 환산합니다. 15×3=45, 15×4=60이니까 50kt인 이번 북한 핵실험 파괴력이 히로시마 원자폭탄 3~4배라는 평가가 자연스레 따라오는 겁니다.

미국 지질조사국(USGS)은 이번 지진 규모를 6.3이라고 발표했습니다. 기상청에서 얻은 공식에 넣어보면 TNT 290kt도 규모 6.3입니다. 이렇게 되면 이번 북한 핵 실험은 리틀보이 보다 20배 가까이 파괴력이 컸다고 할 수 있습니다.

어느 쪽이 맞는지 알 수 없지만 북한이 너무 무모한 일을 저질렀다는 사실만큼은 틀림없습니다.

황규인 기자 kini@donga.com