[理知논술]초등 생각하는 수학

▼ 수와 연산▼

《수학의 기초가 되는 기본적인 사칙연산을 이해하고 이를 응용하는 활동을 통해 체계적이고 논리적인 해결력을 기를 수 있는 영역입니다.》

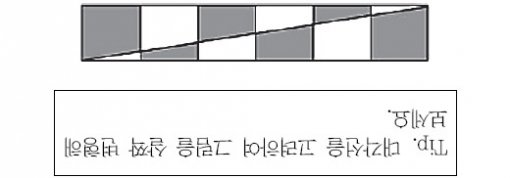
1. 다음 조건을 만족시키는 자리 수를 ㉠㉡㉢㉣㉤이라 할 때, ㉠+㉡+㉢+㉣+㉤의 값은 얼마입니까?

2. 아래의 보기와 같은 자연수를 대칭수라고 부릅니다. 이때 10부터 550까지의 자연수 중에서 대칭수가 아닌 것은 모두 몇 개입니까?

▼ 도형▼

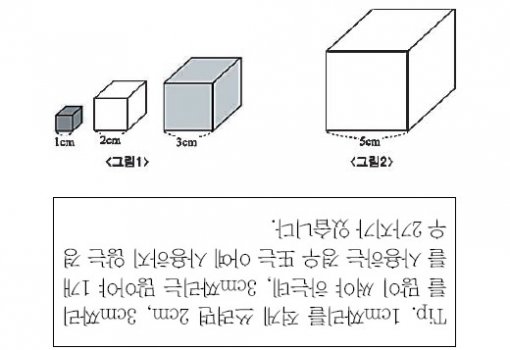
《기본도형을 이해하고, 평면도형과 입체도형에 대한 정확한 인지를 통해 공간 지각력과 논리적 사고력을 기르는 데 도움이 되는 영역입니다.》

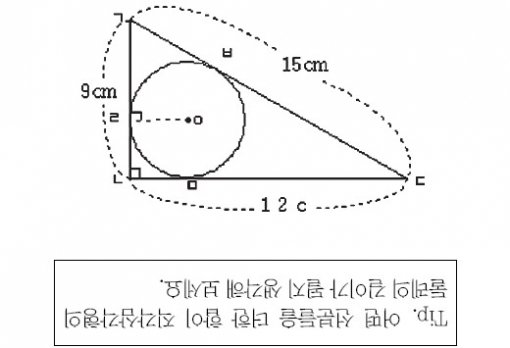
1. 세 변의 길이가 각각 9cm, 12cm, 15cm인 직각삼각형 ㄱㄴㄷ 안에 꽉 차는 원을 그렸습니다. 원과 삼각형의 세 변이 만나는 점을 ㄹ, ㅁ, ㅂ이라 할 때, (선분 ㄱㄹ)=(선분 ㄱㅂ), (선분 ㄴㄹ)=(선분 ㄴㅁ), (선분 ㄷㅁ)=(선분 ㄷㅂ)입니다. 이 원의 반지름의 길이를 구하시오.

2. 다음 그림과 같이 한 눈금의 길이가 1cm인 모눈종이가 있습니다. 각 ㉠의 크기는 얼마입니까?

① 30° ② 35° ③ 40° ④ 45° ⑤ 50°

3. <그림1>에 있는 세 가지 정육면체를 여러 개 쌓아서 한 모서리가 5cm인 <그림2>의 정육면체를 만들려고 합니다. 한 모서리가 1cm인 정육면체를 가장 적게 쓸려고 할 때, 이것은 몇 개 필요합니까?

▼ 측정▼

《길이, 시간, 들이, 무게, 각도, 넓이, 부피, 삼각비 등의 개념을 다루는 가장 현실감 있는 활동 영역으로서 다양한 문제를 접해보는 동안 통합적 사고력을 기를 수 있는 영역입니다.》

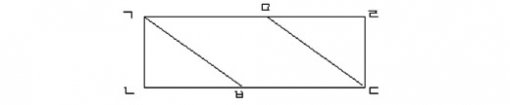
1. 사각형 ㄱㄴㄷㄹ은 가로의 길이가 세로의 길이의 3배인 직사각형이고, 사각형 ㄱㅂㄷㅁ은 마름모입니다. 마름모 ㄱㅂㄷㅁ의 둘레가 40cm이고, 삼각형 ㄱㄴㅂ의 둘레가 24cm일 때, 직사각형 ㄱㄴㄷㄹ의 넓이는 얼마입니까?

①106cm ②107cm ③108cm ④109cm ⑤110cm

2. 다음 그림은 한 변의 길이가 6인 정사각형 6장을 이어 붙여 한 대각선을 그린 것입니다. 색칠된 부분의 넓이는 얼마입니까?

▼ 확률과 통계▼

《자료의 수집과 기준에 따른 분류 및 정리를 통하여 논리적인 판단을 내리는 데 도움이 되는 영역입니다.》

1. 오른쪽 그림과 같이 밑면이 사각형인 뿔 ㄱㄴㄷㄹㅁ이 있습니다. 점 ㄱ을 출발하여 모서리를 따라가면서 각 꼭지점을 모두 한 번씩만 지나서 ㄱ으로 돌아오는 서로 다른 길은 모두 몇 가지입니까?

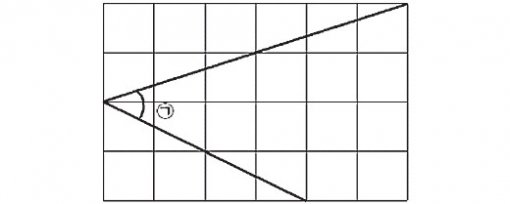
2. 오른쪽 그림은 12개의 점을 같은 간격으로 배열한 점판입니다. 이 점판 위의 네 점을 꼭지점으로 하는 평행사변형을 그릴 때, 두 대각선의 길이가 다른 평행사변형은 모두 몇 개 그릴 수 있습니까? (단, 돌리거나 뒤집어서 겹쳐지는 것들은 하나로 봅니다.)

▼ 문자와 식▼

《여러 가지 상황에서 문제를 스스로 만들어 보거나 다양한 해결 방법을 탐색하고, 새로운 문제로 바꾸어 보는 활동을 통해 창의적인 문제해결력을 기를 수 있는 영역입니다.》

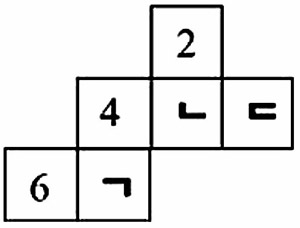
1. 오른쪽 그림은 정육면체의 전개도입니다. 마주 보는 면에 있는 두 수의 합이 모두 7일 때, ㄱ-ㄴ+ㄷ의 값은 얼마입니까?

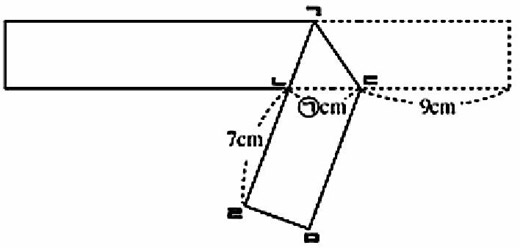
2. 직사각형 종이 띠를 아래 그림처럼 접었더니 사다리꼴 ㄴㄹㅁㄷ의 넓이가 삼각형 ㄱㄴㄷ의 넓이의 4배가 되었습니다. 이때 ㉠의 값은 얼마입니까?

▼ 규칙성과 함수▼

《수학의 조화로운 규칙성을 발견함으로써 수학에 대한 새로운 흥미와 관심을 유발하고 주위 사물을 새로운 눈으로 관찰할 수 있는 안목과 태도를 길러주는 영역입니다.》

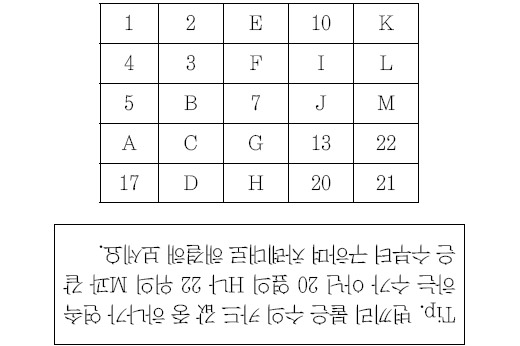
1. 다음은 1부터 25까지의 자연수가 적힌 카드를 연속하는 수의 카드가 변끼리 붙어있도록 배열해 놓은 것입니다. 이때 C와 L의 수를 각각 구하시오.

2. 다음과 같은 규칙으로 수를 써 나가면 102번째의 수는 어느 것입니까?

① 3 ② 5 ③ 6 ④ 8 ⑤ 9

시도교육청·대학부설 영재교육원 초등부 대비 문제 (3∼5학년)

해설 및 정답은 인터넷 이지논술(www.easynonsul.com) 사이트에서 볼 수 있습니다.