

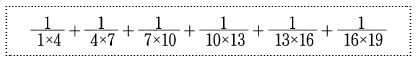

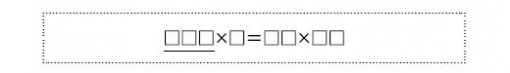

| ○ 네 자리 수입니다. ○ 천의 자리의 숫자와 일의 자리의 숫자를 합하면 10이고 각 자리 숫자의 합은 23입니다. ○ 천의 자리의 숫자는 백의 자리 숫자보다 작고, 백의 자리의 숫자는 십의 자리의 숫자보다 작습니다. ○ 각 자리의 숫자 중 하나는 8입니다. ○ 각 자리의 숫자의 곱은 576입니다. |
| Tip. 구하고자 하는 네 자리 수를 ㉮㉯㉰㉱라고 했을 때, 두 번째 조건으로부터 ㉮+㉱=10이고, ㉯+㉰=13임을 알 수 있습니다. |
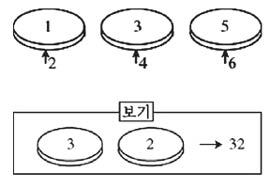
4. [규칙성과 함수] 규칙에 따라 보기와 같이 분수를 늘어놓았습니다. <--이미지-->는 몇 번째에 있습니까?
떤 규칙이 있는지 생각해 보세요.
5. [문자와 식] 일의 자리의 수가 0이 아닌 어떤 두 자리의 자연수가 있습니다. 이 수의 십의 자리의 수와 일의 자리의 수를 바꾼 수는 원래의 수보다 45가 작습니다. 이렇게 되는 원래의 두 자리의 자연수를 모두 찾아서 더하면 얼마입니까?
6. [수와 연산] <--이미지--> 같이 분모가 두 수의 곱으로 표시되는 분수를 다음과 같이 나타낼 수 있습니다.
8. [도형] 가로와 세로가 각각 20cm와 10cm인 직사각형 모양의 타일 4장과 한 변이 10cm인 정사각형 모양의 타일 1장을 이어 붙여서 한 변이 30cm인 정사각형 모양을 만들려고 합니다. 만들 수 있는 모양을 모두 그리시오. (단, 돌리거나 뒤집어서 모양이 같아지는 경우에는 같은 모양으로 생각합니다.)
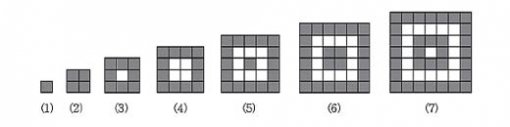
9. [규칙성과 함수] 다음 그림은 어떤 규칙에 따라서 정사각형에 색칠한 모양입니다. 이러한 모양을 계속 만들어 나갈 때 (16)의 모양에서 색칠된 정사각형의 개수를 구하시오.
10. [통합형 심층] 다음 식이 성립하도록 □안에 한 자리 수를 넣으려고 합니다. □□□×□를 계산한 답이 가장 클 때 밑줄 친 세 자리 수는 얼마인지 구하시오.
◇하늘교육 선임연구원 김화자 선생님이 영재교육원 초등부 대비문제를 동영상으로 강의합니다.
◇시도교육청·대학부설 영재교육원 초등부 선발시험 대비 문제(3∼5학년) 해설 및 정답은 인터넷 이지논술 사이트(www.easynonsul.com)에서 볼 수 있습니다.
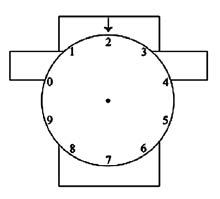
Tip. 십의 자리가 될 수 있는 수는 6, 5, 4, 3입니다. 각각의 경우로 나누어 생각해 보세요. Tip. 이웃한 숫자들이 이루는 각이 몇 도(°)인지 구한 후 제시된 숫자를 찍기 위해 숫자판을 회전시키는 최소의 칸수를 세어 보세요. Tip. 분모가 같은 분수끼리 묶은 다음, 각 묶음에 들어 있는 분수의 개수 사이에는 어 Tip. 두 자리의 자연수에서 십의 자리 수와 일의 자리 수의 차는 5입니다. Tip. 주어진 식을 위 계산 방법에 따라 나열하면 식을 간단히 나타낼 수 있습니다. Tip. 작은 직사각형의 가로 길이는 1/4cm, 세로 길이는 1/6cm입니다. Tip. 나열된 그림들에서 가장 바깥쪽으로부터 홀수 번째 정사각형에 색칠이 되는 규칙을 찾을 수 있습니다. Tip. 주어진 조건으로부터 두 자리 수 중 한 수는 9의 배수이거나 두 수 모두 3의 배수임을 알 수 있습니다.
-
- 좋아요
- 0개
-
- 슬퍼요
- 0개
-
- 화나요
- 0개



댓글 0