[理知논술]논술에 강한 수학

동전 양면 확률 분명히 반반인데

왜 아무리 던지고 던져도

앞뒤 횟수가 달리 나올까

동전을 던지면 앞·뒤가 나올 확률이 반반이다. 따라서 동전을 충분히 많이 던지면 앞·뒤가 나올 확률은 각각 반반이 된다. 그렇다면 우리가 모르는 어떠한 법칙 또는 힘이 동전의 앞·뒤가 나오는 현상에 영향을 미치는 걸까? 예를 들어 100회 던졌을 때 앞이 60번, 뒤가 40번 나왔다면 이후에 동전을 던질 때는 뒤가 나올 확률이 더 높아져야만 우리가 알고 있는 지식이 옳다는 걸 증명할 수 있다. 그러나 처음에 동전을 던질 때는 매번 앞·뒤가 나올 확률이 같다는 전제를 세우고 이론을 전개해오지 않았는가? 어디가 잘못된 것일까? 우선 다음 글을 분석하여 보자.

(가) 확률의 기초를 공부한 학생은 누구나 동전을 던졌을 때 앞·뒤의 확률이 반반이라면 충분히 많은 횟수의 ‘동전 던지기’를 시행했을 때의 앞·뒤의 빈도가 비슷해진다는 것을 알고 있다. 이를 도박에 적용시켜 보자. 한 사람이 동전을 던지고 나는 앞·뒤 중 한 곳에 돈을 건다. 맞혔을 때는 내가 건 돈의 두 배를 받지만 못 맞혔을 때는 돈을 잃게 된다. 단순한 기댓값 계산을 통해 우리는 이와 같은 도박이 ‘정당한 것’임을 알 수 있다. 거기에 처음에 제시한 확률의 빈도를 적용시켜 보는 것이다. 즉, 앞이 연속으로 세 번 나왔다고 하자. 이때 나는 ‘뒤’에다 돈을 건다. 왜냐하면 충분한 횟수의 동전 던지기가 시행된다면 앞·뒤의 빈도가 비슷해져야 함을 알기 때문이다. 이로써 나는 동전 던지기의 도박에서 승률을 높일 수 있다.

위 글에는 분명한 오류가 있다. 오류를 쉽게 찾아낼 수 있다면 확률에 대한 기본적 이해가 탄탄히 되어있는 셈이다. (가)에 숨은 오류는 ‘동전이 앞의 상황을 기억하지 못한다’는 데 있다. 동전을 던져 10번 연속 앞이 나왔다 하더라도 11번째에 동전을 던졌을 때 앞·뒤가 나올 확률은 언제나 반반이다. 이전의 사건이 미래의 사건에 전혀 영향을 줄 수 없는 것이다. 하지만 글 (가)와는 다른 이유로 도박의 승률을 높일 수 있다고 주장하는 다음 글을 보자.

글 (나)에서 잘못된 곳을 찾아내지 못했다면 (가)에 대한 해석을 다시 읽어보기 바란다. (가)에 숨은 오류가 여기서도 동일하게 나타나기 때문이다. 한 가지 덧붙이자면 (나)의 오류는 10회 시행하기 전에는 옳은 말이지만 이미 9번 앞이 나온 상황에서는 엉터리 논증이 된다.

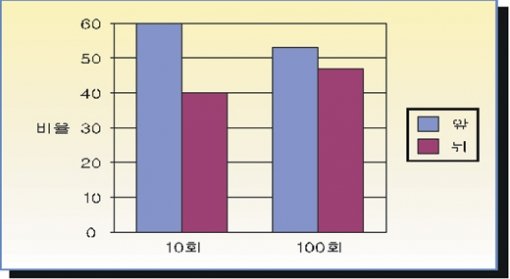
그럼 이제 본론으로 들어가 보자. 글 (가)와 (나)에서 알 수 있듯이 과거의 확률은 미래의 확률에 전혀 영향을 주지 못한다. 그런데 어떻게 ‘충분히 많은 시행을 하였을 경우에 앞·뒤의 비율이 비슷해질 수 있다’는 것일까? 다음 그래프를 보자.

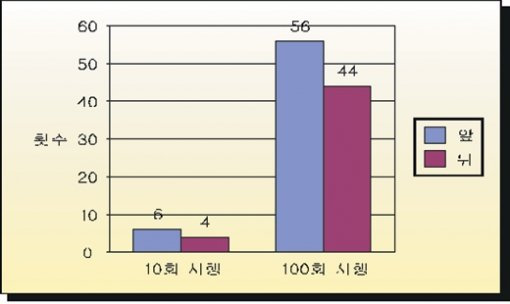
동전 던지기를 10회 시행했더니 동전의 앞이 6번, 뒤가 4회 나왔고 100회 시행했더니 앞이 56번, 뒤가 44번 나왔다고 하자. 비율로는 점점 5 대 5에 가까워진다. 하지만 여기서 우리가 잘못 인식하는 것이 있다. 충분히 많은 횟수를 시행하게 되면 앞·뒤의 비율이 5 대 5에 가까워진다는 말을 동전의 앞·뒤가 나오는 횟수가 같아지는 것이라고 착각하는 것이다.

실제 동전의 앞·뒤가 나올 경우의 수를 살펴보면 알 수 있다. 즉 10회 시행 시에는 동전의 앞이 나오는 횟수와 뒤가 나오는 횟수에 2번의 차이가 난다. 그러나 100회 시행했을 경우에는 12번이나 차이가 난다. 즉, 동전을 많이 던져도 동전의 앞·뒤가 나오는 횟수의 차이가 줄어들지 않는다. 오히려 확률적인 계산에 따르면 차이는 더 벌어질 수밖에 없다.

그러나 비율로 생각해보면 다른 결과가 나온다. 10회 중에 2번의 차이는 100회 중에 12번의 차이보다 비율이 높다. 그리하여 동전을 충분히 많은 횟수로 던지면 앞·뒤가 나오는 비율이 점차 5 대 5에 가까워지는 것이다. 다음 그래프는 위의 그래프의 y축을 좀 더 사실적으로 고친 것이다. 그래프에서 알 수 있듯이 100회 시행에서 앞·뒤의 횟수 차이가 10회 시행에서보다 많이 커진다. 여기까지 이해가 됐다면 처음에 제시한 문제를 꼭 다시 읽어보기 바란다.

횝뵌