[신나는 공부]창의력을 잡아주는 해법수학교실/길의 가짓수

길의 가짓수

길의 가짓수 구하기 문제는 최단경로의 가짓수뿐만 아니라 갈 수 있는 모든 길을 따져야 합니다. 이 유형의 문제는 정형화된 풀이법이 없어 번뜩이는 아이디어가 필요합니다. 영재교육원 시험에서도 상대적으로 출제 빈도가 높은 유형의 문제입니다.

○ Step1< 생각 키우기 >

오른쪽 그림은 작은 정사각형 네 개로 이루어진 도형입니다. 점 A에서 점 B까지 작은 정사각형의 변을 따라서 가는 방법을 구하려 할 때, 물음에 답하시오.(단 같은 점은 여러 번 지날 수 있지만 같은 변은 여러 번 지나서는 안 되며, 반드시 최단경로로 가지 않아도 됩니다)

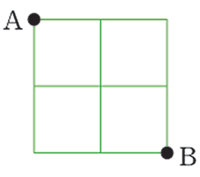
⑴ 점 A에서 점 B까지 가장 짧은 거리로 갈 때 변을 몇 개 지나게 됩니까? 또 가장 긴 거리로 갈 때 변을 몇 개 지나게 됩니까?

⑵ 점 A에서 점 B까지 가는 방법은 변 4개를 지나는 방법, 변 6개를 지나는 방법, 변 8개를 지나는 방법이 있습니다. 각각의 방법이 몇 가지씩 있는지 구하시오.

⑶ 점 A에서 점 B까지 작은 정사각형의 변을 따라서 가는 방법은 모두 몇 가지입니까?

○ Step2< 창의력 넓히기 >

A에서 J까지 10개의 방이 있고, 어떤 방에서 다른 방으로 이동할 때는 화살표 방향대로만 이동할 수 있다고 합니다. A에서 J까지 가는 방법은 모두 몇 가지입니까?

【생각의 흐름】

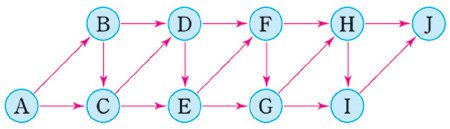
① A에서 B까지 가는 방법과 C까지 가는 방법의 가짓수를 각각 구합니다.

② A에서 D까지 가는 방법은 B에서 바로 가는 방법(방법1)과 C에서 가는 방법(방법2) 두 종류입니다.

즉, (방법1의 가짓수)+(방법2의 가짓수)=(D까지 가는 방법의 가짓수)이고, 방법 1과 2의 가짓수는 각각 B와 C까지 가는 방법의 가짓수와 같다는 점을 이용해 D까지 가는 방법의 가짓수를 구합니다.

③ 같은 방법으로 E까지 가는 방법의 가짓수는 C와 D까지 가는 방법의 가짓수를 합해서 구할 수 있습니다. 이런 방법으로 가짓수를 차례대로 구하여 J까지 가는 방법의 가짓수를 구합니다.

○ Step3< 영재교육원 도전하기 >

어떤 마을에 그림과 같이 도로가 나 있는데, 각 도로는 일방통행이어서 화살표 방향으로만 갈 수 있습니다. 집에서 백화점까지 가는 방법은 모두 몇 가지 있습니까?

☞ 창의력을 잡아주는 해법수학교실에 대한 소감을 작성해 홈페이지에 올려주시면 추첨을 통해 닌텐도 게임기, 문화상품권 등 푸짐한 선물을 드립니다.

● 정답 및 해설 보기: ㈜천재문화/해법수학교실 홈페이지(www.hbmath.co.kr)