[신나는 공부]창의력을 잡아주는 해법수학교실

<지오보드>

지오보드(Geoboard)는 영국의 수학교육자 가테노(C Gattegno)가 개발한 수학교구로 판자 위에 일정한 간격으로 못을 박은 뒤 그 위에 고무줄을 걸어 여러 가지 도형을 구성할 수 있도록 만들어졌습니다.
지오보드를 이용해 도형을 만들다보면 일정한 규칙을 발견할 수 있습니다. 이 규칙을 이용하면 직접 도형을 만들지 않고도 몇 개의 도형을 만들 수 있는지 알 수 있습니다.

● Step1

< 생각 키우기 >
다음 그림과 같은 점판 위에 정사각형을 그리려고 합니다.
크기가 서로 다른 정사각형을 모두 몇 개나 그릴 수 있을까요?
다음 물음에 답하시오.

(1) 점판 위의 굵은 점 하나를 꼭짓점으로 하는 정사각형을 모두 그리시오.

(2) 점판 위의 굵은 점 하나를 꼭짓점으로 하는 정사각형을 모두 그리시오. (단, 위의 (1)번에서 그린 정사각형과 같은 것은 제외합니다)


● Step2

< 창의력 넓히기 >
다음 그림과 같이 원 위에 A, B, C, D, E 5개의 점이 찍혀 있을 때, 원 위의 두 점을 이어 만들 수 있는 선분은 모두 몇 개입니까?

[ 생각의 흐름 ]
① 점 A에선 선분 AB, 선분 AC, 선분 AD, 선분 AE 등 모두 4개의 선분을 만들 수 있습니다.
점 B, C, D, E에서 그을 수 있는 선분의 개수를 각각 구한 뒤 더합니다.

② 점 A에서 그은 선분 AB와 점 B에서 그은 선분 BA는 서로 같은 선분입니다. 이와 같이 위의 ①번에서 구한 값은 모든 경우의 선분을 두 번씩 더한 것과 같습니다. 따라서 위의 ①번에서 구한 값을 반으로 나눠 두 점을 이어 만들 수 있는 선분의 개수를 구합니다.

● Step3

< 영재교육원 도전하기 >
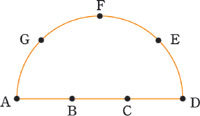
다음 그림과 같이 반원 위에 7개의 점이 있을 때 4개의 점을 이어 그릴 수 있는 서로 다른 사각형은 모두 몇 개입니까?

영재교육원과 특목고를 준비하는 분들을 위해 다양한 창의력 문제를 담은 ‘해법수학 영재교육’(전 9권)을 출간했습니다. 기출 유형 분석을 통한 단계별 32주제 구성, 단계별 탐구 학습프로그램 구현, 1일 1주제 학습으로 9개월이면 유형에서 실전까지 완성할 수 있습니다. 지금부터 대한민국 초등학생들의 영재교육원 합격의 길을 ‘해법수학 영재교육’이 안내합니다.
○ 구입 문의: 02-857-3200 또는 홈페이지(www.hbmath.co.kr)
○ 정답 및 해설 보기: 해법수학교실 (www.hbmath.co.kr)