[신나는 공부]창의력을 잡아주는 해법수학교실

<경기의 경우의 수>

《경기에서 생길 수 있는 다양한 경우를 따지는 문제는 영재교육원 선발시험은 물론 특목고 입시에서 자주 출제되고 있습니다. 또한 이 문제들은 비둘기집 원리, 경우의 수, 짝수와 홀수 등 다양한 문제에 응용되고 있습니다.》

○ Step1
< 생각 키우기 >

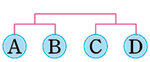
오른쪽 그림은 월드컵 4강에 진출한 4개 팀의 토너먼트 대진표입니다. 경기 결과에 영향을 미치지 않는 대진표를 서로 같은 대진표라고 할 때, 4개 팀을 대진표에 배치하는 서로 다른 방법은 몇 가지인지 구하려고 합니다. 물음에 답하시오.

(1) 4개 팀을 대진표의 A, B, C, D에 차례대로 넣을 수 있는 방법의 수를 구하시오.

(2) A, B의 위치에 들어가는 2개 팀은 위치가 서로 바뀌어도 경기에는 아무런 영향을 미치지 않습니다.

일 경우가 서로 같으므로 전체를 2로 나누어야 합니다. C, D의 경우와 마지막 결승전도 마찬가지입니다. 서로 다른 대진표는 몇 가지입니까?

○ Step2
< 창의력 넓히기 >

10개의 야구 팀이 리그전으로 경기를 하는 데 10개 팀이 모두 한 번 이상은 경기에서 이겼다고 합니다. 10개 팀의 승수가 모두 서로 다를 수 있습니까? 없다면 그 이유를 설명하고, 최소한 몇 개 팀이 같은 승수를 얻게 되는지 구하시오.

【생각의 흐름】

① 10개의 야구 팀은 각각 몇 번씩 경기를 하는지 구합니다.
② 모든 팀이 한 경기 이상은 이겼다고 하였으므로 가능한 승수를 모두 써 봅니다.
③ 10개 팀이 모두 서로 다른 승수를 얻는 것이 가능한지 알아봅니다.
④ 어떤 경우에도 항상 몇 개의 팀은 같은 승수를 가지게 되는지 구합니다.

○ Step3
< 영재교육원 도전하기 >

중국, 일본 두 나라에서 각각 4명씩 모두 8명의 100m 달리기 선수가 출발선에 서 있습니다. 달리기 경주를 시작해서 결승선에 들어오는 등수와 같은 점수를 8명의 선수가 각각 받게 됩니다. 중국과 일본 각 나라 선수들의 점수를 더해 그 합이 더 작은 나라가 이긴다고 합니다. 같은 점수를 받은 선수가 없다고 할 때, 일본 선수들의 점수 합이 몇 점을 넘으면 중국이 일본을 이길 수 있는지 구하시오.

※ 영재교육원과 특목고를 준비하는 분들을 위해 다양한 창의력 문제를 담은 ‘해법수학 영재교육’(전 9권)을 출간했습니다. 기출 유형 분석을 통한 단계별 32주제 구성, 단계별 탐구 학습프로그램 구현, 1일 1주제 학습으로 9개월이면 유형에서 실전까지 완성할 수 있습니다. 지금부터 대한민국 초등학생들의 영재교육원 합격의 길을 ‘해법수학 영재교육’이 안내합니다.

○ 구입 문의: 02-857-3200 또는 홈페이지(www.hbmath.co.kr)
○ 정답 및 해설 보기: 해법수학교실 (www.hbmath.co.kr)