여러가지 개념의 의미-맥락 파악 전에
현실에 먼저 적용시켜 이해하는 과정 필요
‘수학적 사고’란 여러 가지 수학적 개념, 원리, 법칙을 이해한 뒤 수학적 안목을 가지고 문제를 해결하는 과정이다. 수학적 안목이 있으면 문제에 나오는 여러 용어, 기호, 표, 식, 그래프를 쉽게 이해할 수 있다.다음은 농도에 관한 방정식의 대표문항으로 개념을 잘못 이해해 문제를 풀지 못한 경우다.

위 학생은 ‘8%의 소금물 300g에 물을 더 넣었더니(
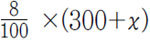
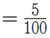

위 문제를 해결하는 관건은 ‘무엇을 같게 놓을 것인가?’이다. 물을 더 넣더라도 변하지 않는 것은 소금의 양이므로, 8%의 소금물에 들어 있는 소금의 양(
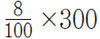
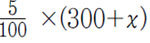
즉, 방정식을 (
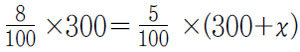

김민식 시매쓰수학연구소 수석연구원
-
- 좋아요
- 0개
-
- 슬퍼요
- 0개
-
- 화나요
- 0개



댓글 0