정재가 학원에서 배운 태권도 품새를 엄마에게 보여줍니다. “태! 권! 도!” “연습을 열심히 하는구나” “네. 열심히 연습해서 빨리 검은 띠를 따고 싶어요. 그래야 올림픽에서 금메달을 따죠.” “안 그래도 기쁜 소식이 있단다. 동아일보 2월 13일자 A1면을 보니 태권도가 2020년 이후에도 계속 올림픽 정식종목으로 남게 됐다는구나.”
“진짜요?” “세계화에 성공했기 때문이래. 태권도는 2000년 시드니 대회 때 처음 정식종목으로 채택돼 런던 올림픽까지 네 차례 올림픽 무대에 올랐단다. 아시아경기대회 등 5개 대륙 종합경기대회에서 정식 종목으로 열릴 만큼 세계화를 이뤘기 때문이야.”
○ 각도의 유래
정재는 태권도를 열심히 배우는 중입니다. 540도 돌려차기를 멋있게 하겠다고 말합니다. 몇 바퀴를 돌아야 가능할까요? 각도에 대해서 공부하면 됩니다.
천문학자들은 태양이 뜨는 장소가 매일 조금씩 움직여 360일이 지나면 똑같은 장소로 돌아간다는 점을 확인했어요. 그래서 원 모양으로 한 바퀴 움직인 각을 360도라고 한답니다. 태양의 모양인 원을 360등분 했는데, 그 중 하나를 1도(1°)라고 정했다는군요. 원 모양으로 한 바퀴 움직인 각도가 360도니까 반 바퀴는 360÷2=180도예요. 360도에다가 180도를 더하면 540도가 됩니다. 540도 돌려차기를 하려면 한 바퀴 하고도 반 바퀴를 더 돌아야 하겠죠?
별과 태양의 움직임에서뿐만 아니라 우리 주위에서도 여러 크기의 각을 찾아볼 수 있답니다. 나침반은 각의 크기를 이용하여 방향을 알 수 있게 해주는 기구입니다. 북쪽을 기준으로 시계방향으로 90도 돌면 동쪽이고, 여기에서 다시 시계방향으로 90도 돌면 남쪽, 또다시 90도 돌면 서쪽, 그리고 90도를 더 돌아 모두 360도를 돌면 처음의 북쪽이지요.
각의 크기를 각도라고 합니다. 각도를 나타내는 단위는 1직각과 1도가 있습니다. 1직각을 똑같이 90으로 나눈 하나를 1도라 하고 1°라고 씁니다. 각도의 합과 차는 자연수의 덧셈, 뺄셈과 같은 방법으로 계산하고, 계산 결과에 도(°)를 붙이면 됩니다.
○ 문제 풀이
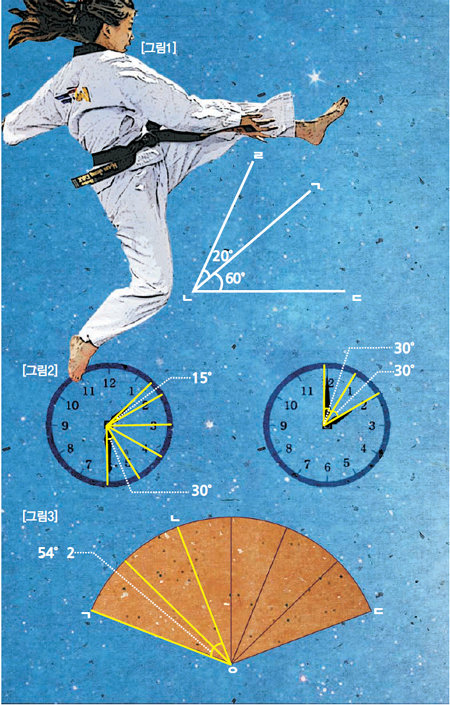
최고로 높이 발로 찬 발차기의 각은 <각 ㄹㄴㄷ>입니다. 이 각의 크기는 <각 ㄱㄴㄷ>의 크기와 <각 ㄹㄴㄱ>의 크기를 더한 수치와 같습니다. 즉 60+20=80도입니다. 정재의 발차기 최고 기록은 80도입니다.
두 번째 문제를 풀어볼까요? 정재는 오후 1시 30분부터 2시까지 태권도 연습을 했습니다. 시계에서 긴 바늘과 짧은 바늘이 이루는 작은 쪽의 각의 크기의 합과 차는 몇 도일까요? <그림2>
답을 구하려면 연습을 시작한 시각의 두 바늘 사이의 각도와 연습이 끝난 시각의 두 바늘 사이의 각도를 구해야 합니다. 기억나나요? 원의 각도가 얼마인지? 맞아요, 360도예요. 시계는 12칸으로 나뉘어 숫자 1부터 12까지 쓰여 있어요. 그래서 숫자 사이 1칸의 각도는 360÷12=30도이지요. 즉 긴바늘이 시계를 1바퀴(360도) 도는 동안 짧은바늘은 30도 움직입니다.
연습을 시작한 시계에서 긴바늘은 숫자 6을 가리키고, 짧은바늘은 숫자 1과 2 사이에 있어요. 숫자 2에서 6까지는 4칸으로 30×4칸=120도이고 짧은바늘에서 숫자 2까지는 30÷2=15도입니다. 따라서 연습을 시작한 시계의 긴바늘과 짧은바늘 사이의 작은 각의 크기는 120+15=135도예요.
이번엔 연습이 끝난 시계의 긴바늘과 짧은바늘 사이의 작은 각의 크기를 구하기로 해요. 숫자 12에서 숫자 2까지는 2칸으로 30×2=60도입니다. 아, 이걸로 다 끝난 게 아니에요. 문제에서 구하라는 말한 답은 두 각의 크기의 합과 차이니까요. 답은 두 각의 크기의 합 135+60=195도, 두 각의 크기의 차 135-60=75도입니다.
마지막으로 하나 더 풀어요. 연습을 끝내고 정재는 땀을 뻘뻘 흘렸습니다. 너무 더워 시원하게 부채질을 하려고 합니다. 부챗살과 부챗살 사이의 각도가 모두 같고 <각 ㄱㅇㄴ>의 크기가 54도라면 <각 ㄱㅇㄷ>은 몇 도입니까?
<각 ㄱㅇㄴ>의 크기가 54도입니다. 부챗살 한 칸의 크기는 54÷2=27도입니다. 부채가 활짝 펼쳐졌을 때의 <각 ㄱㅇㄷ>은 부챗살이 몇 칸일까요? 6칸입니다. 그러므로 부챗살과 부챗살 사이의 각도는 27×6=162도입니다. <그림3>
김성희 웅진씽크빅 씽크U수학 개발팀 책임연구원
신문과 놀자!(초중고생을 위한 NIE) >
구독
이런 구독물도 추천합니다!
-

양종구의 100세 시대 건강법
구독
-

사설
구독
-

내가 만난 명문장
구독
-
- 좋아요
- 0개
-
- 슬퍼요
- 0개
-
- 화나요
- 0개
-
- 추천해요
- 개
![[신문과 놀자!/함께 떠나요! 세계지리 여행]겨울엔 낮에도 컴컴… 극야 현상, 우울증 원인 되기도](https://dimg.donga.com/a/180/101/95/2/wps/NEWS/IMAGE/2024/11/18/130449855.9.jpg)

![[사설]“美와 갈 데까지 가봐”… 김정은의 뻔한 ‘도발 후 협상’ 카드](https://dimg.donga.com/a/464/260/95/1/wps/NEWS/FEED/Donga_Home_News/130492910.1.thumb.jpg)

댓글 0