[신문과 놀자!/눈이 커지는 수학]수학이 미술을 만나면… 시각적 사고가 ‘쑥쑥’

서영이는 방학이 되자 그동안 보이지 않았던 체험 및 전시 등에 대한 안내가 눈에 들어왔습니다. 학기 중에 가보지 못했던 미술관과 공연을 이번 방학에 부지런히 다녀보기로 했습니다.

엄마: 서영아, 이번 방학에는 미술전에 같이 가보자. 좋은 전시가 많은 것 같아.

서영: 네. 저도 학교에서 배웠던 저명한 예술가들의 작품을 전시한다는 보도를 봤어요. 예술가들은 정말 대단한 거 같아요. 자신의 생각을 다양한 그림과 작품으로 보여 주잖아요.

엄마: 예술가만 그런 건 아니란다.

서영: 네?

엄마: 수학자들도 고대부터 그림을 많이 사용했단다. 말로 길게 설명하는 대신에 적당한 그림을 제시하고, 시각적인 직관에 근거한 추론을 돕기 위해서였어.

수학에서 그림 그리기

아주 초창기부터 우리가 잘 알고 있는 이집트 상형문자, 그리스어 라틴어 영어 등으로 대표되는 ‘자연어’와 +, ―, ×, ÷ 등의 ‘기호 언어’, 그리고 ‘그림’이 함께 복합적으로 융합되면서 수학이 발전해 왔습니다. 가령 기원전 1850년경 고대 이집트의 수학을 보여주는 모스크바 파피루스는 당시의 글과 기호와 함께 사다리꼴이 그려져 있습니다([그림 1] 참조).

처음 수학에 사용된 그림은 이야기를 보조하는 수단이었지만 점차 수학의 특성을 보여주는 고차원적인 그림을 찾아볼 수 있게 됩니다.

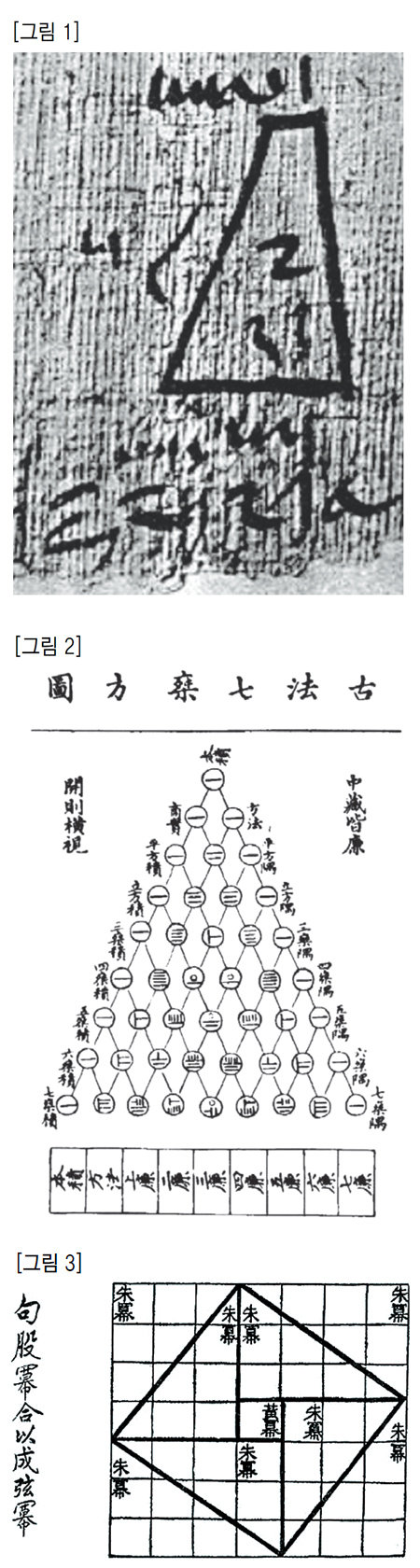
중세 중국의 문헌을 보면 지금의 파스칼의 삼각형(파스칼의 삼각형은 다음과 같이 만듭니다. 먼저 첫 번째 줄에는 숫자 1을 씁니다. 그 다음 줄을 만들려면 바로 위의 왼쪽 숫자와 오른쪽 숫자를 더합니다. 예를 들어 네 번째 줄의 숫자 1과 3을 더하여 다섯 번째 줄의 4가 만들어집니다)이라고 부르는 삼각형 모양의 수 배열이 나타나고, ‘직각삼각형에서 빗변의 제곱은 다른 두 변의 제곱의 합과 같다’는 피타고라스 정리가 나타난 그림도 보입니다([그림 2] [그림 3] 참조).

더 나은 그림을 만들기 위한 노력은 도형을 다루는 기하학의 여러 분야를 발전시켰습니다. 16세기 요하네스 케플러는 정교한 그림과 함께 다양한 다면체와 입체도형을 찾아내기도 했고, 원근법의 발달과 함께 다면체 연구가 촉진되기도 했습니다.

오늘날의 과학 기술은 증강현실이나 가상현실, 3D 프린팅 기술 등 눈으로 보는 이미지의 발전과 함께 과학기술을 이용해 그림과 관련한 어려운 문제를 해결하는 계산기하학과 같은 새로운 수학 분야의 발전을 불러왔습니다.

시각적으로 사고하기

수학은 엄밀함을 추구하는 학문이지만 실제로 수학을 공부하거나 연구하기 위해서는 시각적으로 사고하는 방법을 개발하는 것이 도움이 됩니다. 수학의 성질을 발견하는 데 있어 내부적인 시각화가 중요한 역할을 하며 어떤 경우에는 새로운 연구의 시작이 될 수도 있습니다. 시각화는 시각적인 사고를 발전시키면서 어떠한 이미지(그림, 물체, 그래프, 도형 등)를 만들어 내는 과정을 말합니다. 이러한 과정은 가정과 결론을 바탕으로 추론하는 과정에서 중요한 역할을 하며, 적극적으로 탐구해 본질을 파악하고, 단순화하고 분석하며 종합해 문제를 푸는 과정이라고 할 수 있습니다. 재미있는 수학적 이미지는 시각적인 사고 과정의 독창성과 창의성을 증진시킬 수도 있을 것입니다.

박지현 반포고 교사