[신문과 놀자!/눈이 커지는 수학]바둑돌을 놓는 방법의 수가 10의 170제곱?

바둑 속 수학 원리

9일부터 15일까지 서울에서 인터넷기업 구글의 인공지능 프로그램 ‘알파고(AlphaGo)’와 세계 최강의 바둑기사 이세돌 9단(33)의 대국이 있었습니다. 대국 전부터 알파고의 성능과 승리 확률을 두고 많은 이야기가 나왔습니다. 결국 세기의 대국에서 1승 4패로 우승 타이틀을 알파고에 넘기며 여러 가지 뒷이야기를 남겼습니다. 상훈이는 방송과 신문에서 접했던 바둑판 위에 바둑돌을 놓는 방법의 수에 대해 궁금증이 있었습니다.

상훈: 대국 전에는 바둑판에 바둑돌을 놓는 방법의 수가 상상하기 어려울 정도로 많기 때문에 알파고의 승리가 어려울 것이라는 이야기가 나오기도 했잖아요.

엄마: 그래, 그랬지. 그래서 알파고의 승리에서 가장 눈에 띈 것은 인공지능 기술력이 아니라 컴퓨터 정보처리 속도의 발전이라는 이야기도 있단다. 많은 경우의 수를 다 따지기가 어려운 만큼 알파고는 바둑판의 정보를 습득하고 여러 번의 반복학습을 거쳐 방대한 양의 데이터를 순식간에 검토해 최선의 수를 두는 방식을 이용했단다. 그래도 처리한 정보의 속도와 양은 대단한 것이지.

상훈: 신문에서 바둑돌을 놓는 방법의 수가 약 10의 170제곱이나 된다고 본 것 같아요. 어떻게 그렇게나 많은 경우의 수가 나오나요?

엄마: 아주 큰 수가 분명하지. 바둑돌을 놓는 정확한 경우의 수라고는 말할 수는 없지만 바둑판이 많은 교차점으로 이루어진 격자 판이라는 것과 각 점에 놓을 수 있는 바둑돌의 경우의 수 때문에 그런 결과가 나온 것이란다. 그럼 어떻게 그 결과가 나왔는지 알아볼까?

○ 바둑돌 놓기, 착수의 경우의 수

어떤 일이 일어날 수 있는 경우의 가짓수를 ‘경우의 수’라고 합니다. 그럼 바둑판의 교차점 위에 바둑돌을 놓는 것, 즉 착수의 경우의 수를 생각해 보지요.

우선 간단한 경우부터 생각해 봅시다. 먼저 가로와 세로줄이 1개씩인 하나의 교차점 위에 바둑돌을 놓을 수 있는 경우의 수는 아무것도 놓지 않은 경우, 검은 돌을 두는 경우, 흰 돌을 두는 경우의 세 가지가 있습니다.

[그림 1]

이번에는 가로와 세로 줄이 모두 2개씩인 격자를 생각해 봅시다. 교차점이 2×2=4이고, 각각의 점에 바둑돌을 놓을 수 있는 경우의 수가 3가지씩 있으므로 총 착수의 경우의 수는 3×3×3×3=81가지가 됩니다.

[그림 2]

그러나 바둑에서는 상대방 집에는 돌을 놓을 수 없다는 규칙이 있습니다. 따라서 [그림 3]의 왼쪽과 같이 흰 돌 두 개로 집을 지은 상태라면 검은 돌은 놓을 수 없으며, [그림 3]의 오른쪽 그림과 같이 검은 돌 세 개로 집을 지은 상태에선 흰 돌을 놓을 수 없어, 이러한 경우는 착수의 경우의 수에서 제외해야 합니다.

[그림 3]

이와 같이 착수가 불가능한 경우의 수가 2×2 격자 판에서는 모두 24가지 있으며 81가지에서 24가지를 빼면 총 57가지의 경우의 수가 됩니다. 이는 전체 81개의 경우에서 70%에 해당하는 것이지요.

[그림 4] 2×2 격자 판 위에서 착수가 불가능한 모든 경우

오늘날 우리가 일반적으로 사용하는 바둑판은 가로줄과 세로줄이 모두 19개씩입니다. 따라서 바둑돌을 놓을 수 있는 교차점의 수는 19×19=361개입니다. 같은 방법으로 교차점의 수가 증가될 때 착수의 경우의 수를 구할 수 있습니다. 네덜란드 컴퓨터 과학자 존 트롬프는 착수의 경우의 수를 구하기 위한 효과적인 수학적 알고리즘을 찾는 데 노력해 바둑판의 격자가 2×2인 것에서부터 19×19인 것까지 바둑판 위에 착수의 경우의 수를 구했습니다.

표를 보면 격자 판의 크기가 커질수록 착수의 경우의 수는 급격하게 늘어납니다. 그에 비해 착수의 비는 점점 줄어드는 것을 알 수 있습니다. 바둑판의 모양이 19×19인 격자 판의 경우, 착수의 경우의 수는 교차점에서 가능한 경우의 수에 착수의 비율을 곱한 3361×0.01196으로 약 2.082×10170이 되어 아주 큰 수임을 알 수 있습니다.

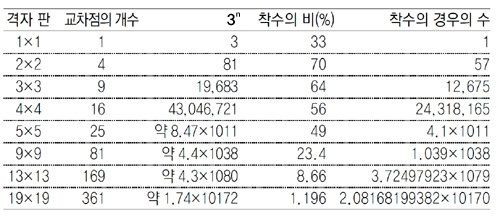
그러나 이 수는 검은 돌과 흰 돌을 번갈아 놓는다는 규칙을 고려하지 않고 검은 돌과 흰 돌이 놓일 수 있는 모든 경우의 수를 구한 것으로 실제 바둑에서 나타나는 경우의 수는 이보다 작게 됩니다.

한편 알파고가 착수하는 방식은 위에서 살펴본 경우의 수를 모두 계산한 것이라기보다는 기존에 잘 알려진 바둑의 착수에 대한 정보, 프로와의 대국의 정보, 자기 자신이 게임을 하여 얻은 정보 등을 학습한 후, 바둑의 고수들이 어디에 많이 놓는지를 분석하고 여기에 놓았을 때 이길 확률이 얼마나 될지 승률을 계산하여 최선의 수를 찾는 방식입니다. 이 역시 수학을 포함하지요.

바둑 자체도 흥미로운 게임이지만, 그 이면의 수학적 원리와 배경을 찾는 일도 흥미롭고 도전적인 일입니다. 인공지능을 시험하는 알파고가 바둑을 선택한 이유도 아마 그런 이유가 아닐까요?

박지현 반포고 교사