[신문과 놀자!/눈이 커지는 수학]0과 1로 나타내는 통신 언어… 그 속에 숨은 수학 원리는?

25일 서울 마포구 KT 아현지사에서 화재로 소실된 케이블 복구 작업이 한창이다. 24일 오전 11시 아현지사 건물 지하 통신구에서 발생한 화재는 오후 9시 진화될 때까지 10시간 동안 16만8000여 개의 유선회선과 광케이블 일부를 태웠다. 이 때문에 유·무선 전화가 불통되고 카드 결제가 안 되는 등 시민들의 일상이 사실상 마비되는 ‘통신대란’을 겪었다. 뉴시스

얼마 전 한 통신사의 통신구 화재가 있었습니다. 복구 작업에도 불구하고 시민들은 유·무선 전화와 인터넷 통신이 끊겨 적잖은 불편을 겪었습니다.

상훈: 통신은 눈에 안 보이는 줄 알았는데 화재로 먹통이 돼 놀랐어요.

엄마: 이번 화재가 난 곳은 통신망의 허브 역할을 하는 곳 중 하나였단다. 그나저나 컴퓨터나 통신 기호가 0과 1로 돼 있는 거 아니?

상훈: 컴퓨터가 0과 1의 기호로 프로그래밍 돼 있다는 것 정도는 알아요.

○ 정보의 단위, 비트

정보를 설명할 때는 ‘비트(bit)’라는 용어를 사용합니다. 이 비트는 정보를 전송할 때 사용하는 이진법, 즉 0과 1만을 사용하는 것을 뜻하는 일종의 단위입니다. 정보 전달의 기본적 원리를 이해하기 위해 한 컴퓨터가 1에서 50까지의 숫자 중 한 숫자를 다른 컴퓨터에 전달한다고 가정해 봅시다. 이때 전송받는 컴퓨터는 그 숫자를 정확히 알기 위해 전송한 컴퓨터에 얼마나 많은 질문을 해야 할까요?

상호 통신에 있어 필요한 정보의 양은 결국 그 대상을 알기 위해 ‘예’ 또는 ‘아니요’로 대답할 수 있는 질문의 횟수에 달려 있습니다. 즉 정보의 비트 수는 질문 횟수와 같은 것입니다. 이때 ‘예’ 또는 ‘아니요’는 각각 1과 0으로 대응됩니다.

그러면 간단한 정보에 대한 비트 수를 실제로 구해 볼까요? 먼저 한 사람은 1에서 20 사이의 숫자를 선택합니다. 다른 사람은 그 숫자를 추측할 수 있을 때까지 “예” 또는 “아니요”라고 답할 수 있는 질문을 합니다. 모든 질문에 “아니요”라는 답은 ‘0’으로 기록하고, “예”라는 답은 ‘1’로 기록합니다. 예를 들면 다음과 같습니다.

이 과정을 반복하다 보면 1에서 20 사이의 숫자 중 하나를 맞히려면 보통 4∼5개의 질문이 필요함을 알 수 있습니다. 이때 숫자 열은 질문의 수와 응답 순서를 나타냅니다.(숫자 열 0100: 질문의 수는 4회, 응답 순서는 ‘아니요, 예, 아니요, 아니요’) 숫자 열의 개수가 4개라면 4비트가 소요됩니다.

○ 정보 수학

이를 좀 더 수학적으로 생각해 봅시다. 우리가 선택할 수 있는 항목의 수를 n으로 나타내보죠. 앞서 살펴본 예에서 1∼20의 숫자 중 하나를 고를 수 있도록 했으므로 선택할 수 있는 항목, 즉 n=20이 됩니다. 이제 n과 이 정보를 전달하는 데 필요한 비트 수 사이의 관계를 찾아봅시다.

f(n)은 n개의 항목 중 하나의 항목을 지정하는 데 필요한 정보 비트 수, 즉 0 또는 1의 개수를 나타냅니다. 예를 들어 f(2)=1이고 f(1)=0입니다. 왜냐하면 n=2, 1과 2 중 하나를 찾아야 할 때는 질문을 한 번만 하면 됩니다. n=1일 때는 아예 질문할 필요가 없습니다. 그럼 f(50)은 50개 중 하나의 항목을 식별하는 데 필요한 비트 수를 의미합니다. 이때 n이 커지면 당연히 비트 수 f(n)도 커지겠지요. 따라서 n〈m이라면 f(n)〈f(m)이 됩니다.

f(n)은 또 다른 성질이 있습니다. 예를 들어 f(8)을 두 개의 그룹으로 나눈 뒤 우선 f(2) 비트를 사용해 두 개 그룹 중 어떤 그룹에 선택한 항목이 있는지 식별할 수 있습니다. 이어 f(4) 비트를 사용해 해당 그룹 내 항목을 식별할 수 있겠죠. 이를 식으로 나타내면 f(8)=f(4×2)=f(4)+f(2)가 됩니다. 다른 경우에도 똑같이 적용할 수 있으므로 f(m×n)=f(m)+f(n)이 됩니다. 위와 같은 성질을 모두 요약하면 다음과 같습니다.

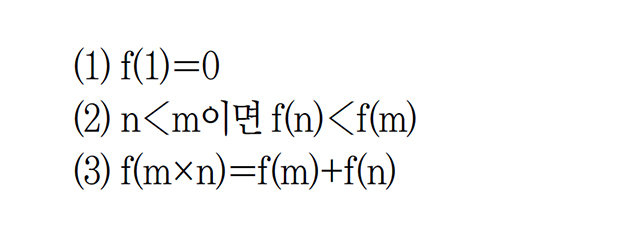
이 모델은 n개의 동일한 가능성을 가진 항목에서 올바른 하나를 찾는 데 필요한 정보의 수, 즉 비트라는 정보의 기본 단위에 관한 것입니다. 정보 이론의 수학은 이와 같은 아이디어로 시작합니다. 이를 확장하면 동일한 가능성이 있다고 가정되지 않은 결과나 오류의 가능성이 응답을 오염시키는 상황까지 적용할 수 있습니다.

정보통신이 곧 생활인 시대에 살고 있는 이때 이용만 하기보다 잠시 멈추고 그 속에 숨어 있는 수학 원리에 관심을 가져보면 어떨까요.

박지현 반포고 교사