[신문과 놀자!/눈이 커지는 수학]매트리스를 오래 사용하려면… “수학으로 풀어보세요”

신종 코로나바이러스 감염증(코로나19)으로 초중고교 개학이 연기되고 학원이 휴원하면서 학생들이 집에 있는 시간이 늘어났습니다. 서영이네는 이 기회에 온 가족이 봄맞이 집 안 청소를 하며 주말을 보냅니다.

서영: 책장을 거실로 옮기고 책상을 꺼내 놓으니 집 안이 카페 분위기가 나네요.

엄마: 그렇지? 대청소를 하는 김에 네 침대 매트리스도 뒤집으려 했단다.

서영: 침대 매트리스를 뒤집어요?

엄마: 응. 일정 기간이 지나면 한쪽만 움푹 파인 자국이 남거든. 그런데 서영아. 침대 매트리스를 뒤집는 방법에도 수학적 원리가 숨어 있다는 사실, 알고 있니?

○침실 안의 군론(群論·group theory)

사람마다 자는 모습은 제각각입니다. 침대 매트리스가 그것을 보여주지요. 어떤 사람은 베개를 겹겹이 쌓아 베거나 밤새도록 이리저리 굴러다니면서 자기 때문에 매트리스에 파인 자국이 거의 남지 않습니다. 또 어떤 사람은 똑바로 누워 미라처럼 꼼짝도 하지 않고 자기 때문에 누운 자리에 움푹 파인 자국이 남습니다. 그래서 매트리스를 오래 사용하기 위해서는 뒤집어가며 사용하라는 권고가 나옵니다.

그런데 침대가 골고루 닳도록 하려면 매트리스를 어떻게 뒤집는 것이 좋을까요? 이 문제를 수학적으로 생각해 봅시다. 수학의 세계에는 ‘침실 안의 군론’이라는 표현이 있습니다. ‘군(group)’이란 것은 쉽게 말하면 침대 프레임에 딱 들어맞도록 매트리스를 뒤집거나 회전시킬 수 있는 모든 경우의 수를 말합니다. 이런 군을 다루는 이론을 ‘군론(group theory)’이라고 하죠.

군론은 단체 댄싱의 안무에서부터 입자물리학의 기본 법칙, 화학의 분자 구조나 결정, 알람브라 궁전의 모자이크에 이르기까지 다양한 분야에서 활용되고 있습니다. 군론 연구자들은 어떤 물체가 지닌 속성을 유지하면서 일부를 변화시킬 수 있는 방법을 고민합니다. 더 정확하게 말하자면 ‘형태를 바꾸지 않으면서 만들어낼 수 있는 모든 변화’를 연구하죠. 이런 변화를 넓은 의미에서 ‘대칭’이라고 부르기도 합니다. 이 변화들을 모아놓으면 ‘군’이 만들어지는 거죠.

매트리스를 예로 들어 볼까요? 침실의 군론은 ‘매트리스의 구조를 유지하면서 방향을 바꾸는 것’을 말합니다. 군론의 조건을 충족하려면 변화가 일어난 후 매트리스가 직사각형 침대 프레임에 딱 들어맞아야 하죠.

○매트리스를 뒤집는 네 가지 군론

이제 침대 매트리스 뒤집을 때 어떤 방식이 군에 포함될 수 있을지 살펴볼까요? 첫 번째는 아무것도 하지 않는 방법입니다. 즉, 매트리스를 있는 그대로 전혀 손대지 않고 내버려 두는 거죠. 이 방법은 매트리스를 오래 쓰는 데는 별 도움이 되지 않겠지만 군에서는 아주 중요한 구성원입니다. 이는 수의 덧셈에서 0, 곱셈에서 1이 하는 역할을 하지요. 수학자들은 이것을 항등원(identity element)이라 부르고 ‘I’라는 기호로 표기합니다.

이제 매트리스의 방향을 바꾸는 방법은 세 가지가 남습니다. 각 방법들을 구분하기 위해서 ＜그림1＞처럼 앞면에는 ‘A’가, 뒷면에는 ‘B’가 쓰인 매트리스가 있다고 생각해 봅시다. 먼저 수평 방향으로 뒤집어 보는 방법을 생각할 수 있습니다. 매트리스의 세로축을 중심으로 180도 회전시킨다고 상상해 보세요. A가 바르게 보이던 매트리스는 B가 바로 보이게 됩니다. 이렇게 수평 방향으로 뒤집는 것을 수평(horizontality)이란 의미에서 ‘H’라고 부르기로 합시다.

좀 더 어려운 방법은 매트리스의 가로축을 중심으로 수직 방향으로 뒤집는 것입니다. 즉, 매트리스를 긴 쪽으로 똑바로 세운 후 그대로 밀어 거꾸로 뒤집는 방법이지요. 이것을 수직 방향 뒤집기라 하고 수직(verticality)의 의미에서 ‘V’라고 하죠. 이렇게 뒤집으면 A가 바르게 보이던 매트리스는 B가 뒤집혀 보이게 됩니다.

마지막 방법은 매트리스를 평평한 상태로 유지한 채 반 바퀴 회전시키는 것입니다. 이 변환은 회전(rotation)의 의미로 ‘R’라고 하지요. 이때 R 회전은 앞서 H와 V 뒤집기와 달리 윗면이 그대로 남아 있게 됩니다. 바르게 보이던 A만 거꾸로 보이게 되는 것이죠.

각 변화들 사이에서 특수한 관계성을 찾아볼 수도 있습니다. ＜그림2＞의 세 번째 그림에서 좌측의 침대를 처음 원래 상태라고 합시다. 여기서 우측을 향한 화살표는 R의 행동을 나타냅니다. 이 화살표는 양방향인데, 처음 상태에서 R를 두 번 하면 다시 원래 상태로 돌아와 아무 행동도 하지 않은 것과 같게 된다는 걸 의미하죠. 이 성질을 기호로 ‘RR=I’로 나타낼 수 있습니다.

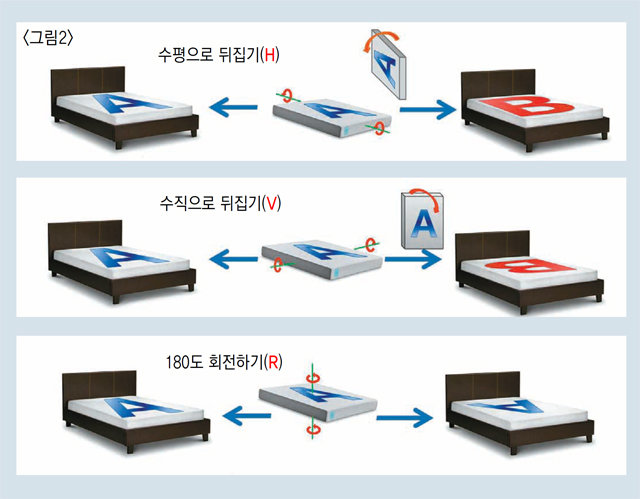
같은 방법으로 ‘VV=I’ ‘HH=I’라는 관계식도 성립한다는 사실을 알 수 있습니다. 또 수직 방향으로 뒤집은 상태가 수평 방향으로 뒤집은 후 180도 회전을 한 결과와 같다는 것도 보여 줍니다. 즉, ‘V=HR’라는 등식도 성립한다는 걸 알게 되죠.

○봄에 회전시키고 가을에 뒤집자

이제 매트리스를 가장 균일하게 닳도록 뒤집는 방법을 찾아볼까요? 네 가지 상태를 골고루 사용하는 전략이 있을 텐데요, 이를 위해서는 네 가지 방법을 주기적으로 돌아가면서 수행하는 방법이 있을 겁니다.

더 좋은 방법은 없을까요? 앞서 살펴본 매트리스 관계식을 생각해보면 R와 H를 교대로 반복하는 전략이 더 편리하다는 사실을 알 수 있습니다. 이는 V를 생략하는 방법이라 크게 힘들이지 않으며 네 가지 상태를 골고루 적용할 수 있습니다. 결국 “봄에는 회전시키고 가을에는 뒤집는다”는 원칙을 세워 보면 매트리스를 오래 쓸 수 있겠습니다.

오랜 집 안 생활에 활기도 떨어지고 답답해지기 쉬운 시기입니다. 봄맞이 집 안 청소를 하면서 동시에 수학적 아이디어도 생각해 보면 어떨까요? 즐거운 마음과 건강한 몸으로 코로나19를 함께 이겨냈으면 좋겠습니다.

박지현 반포고 교사