[신문과 놀자!/눈이 커지는 수학]‘대칭’ 속 균형미와 조화… 가을 풍경에서 찾아볼까요?

동네 가로수 길도 어느새 단풍이 한창이고 11월에 단계적 일상 회복과 함께 늦가을 단풍으로 유명한 숨은 장소와 호젓한 걷기 여행에 대한 뉴스가 최근 들어 속속 눈에 들어옵니다. 상훈은 조심스레 가을 가족 산행을 제안해봅니다.

상훈: 어느새 우리 집 주변이나 학교에도 단풍이 물들어 너무 아름다워요. 이번 주말에는 가족끼리 가까운 산에 가서 단풍을 즐겨도 좋을 듯해요.

엄마: 그래 오랜만에 산행도 좋고, 자연에서도 우리 주변의 여행지에서도 수학을 즐길 수 있겠구나.

○ 선 대칭으로 즐기는 가을 여행

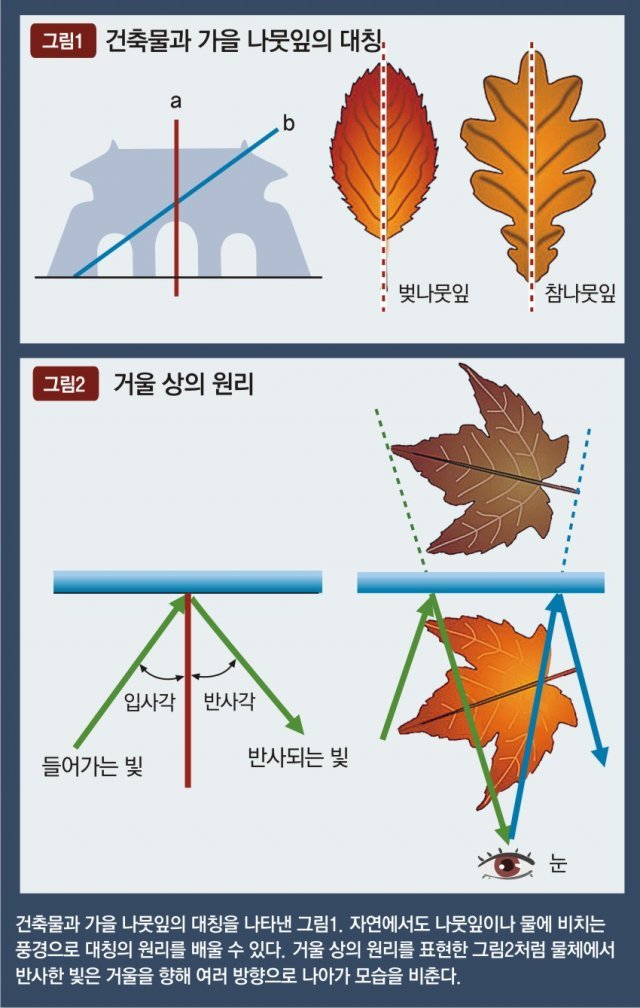
오래된 절이나 궁터에 들어서면 엄숙함과 조화로움에서 오는 따뜻함과 경외감을 느낄 수 있습니다. 건축물이나 자연에서 나오는 이 위엄과 조화는 좌우 대칭이 가져오는 안정성과 통일감, 구조의 조화에서 뿜어져 나오는 아름다움 때문이기도 합니다. 여기서 말하는 대칭이란 물체를 반으로 나누었을 때 그것이 똑같은 모양인 경우를 말합니다. 건축물은 ‘그림1’처럼 중심을 지나는 선 a를 따라 자르면 건물은 대칭을 이루고, 선 b로 자르면 대칭을 이루지 않는 것을 알 수 있습니다. 엄밀한 좌우 대칭은 아니지만 자연에서도 숲이나 산에 떨어진 나뭇잎이나 멀리 물에 비치는 풍경을 통해 또 다른 대칭을 발견할 수 있습니다.

○ 연못과 거울이 만드는 대칭

특히 기암괴석이 비치는 강이나 가로지르는 돌다리 등이 비치는 연못 등을 멀리서 바라볼 때는 풍경이 두 배가 된 듯 지면 위의 풍경을 바라보는 것과는 또 다른 정취를 느낄 수 있습니다. 어떤 경우는 서로 대칭이 된 모습이 하나의 형상이 되어 우리에게 또 다른 형태로 보이기도 합니다.

자연에서의 물은 일종의 거울 역할을 합니다. 우리 선조는 수면에 비친 거울 상을 통해 처음으로 자신의 모습을 보았을 것입니다. 처음으로 사용된 거울인 물거울은 오래지 않아 휴대하기 편한 금속 거울로 발전하였고, 이후 유리 거울이 발명되어 이제는 대중적이고 유용한 도구가 되었습니다. 물체의 거울 상은 면대칭과 관련이 있습니다. 거울 표면을 경계로 거울 앞의 세계가 고스란히 거울 속에 옮겨지는 것이지요.

이것을 대칭변환 또는 대칭이동이라 합니다. 거울을 통한 대칭은 흔히 좌우 반전으로 나타납니다. 우리가 오른손을 들면 거울 속의 나는 왼손을 들고, 우리가 왼손을 들면 거울 속의 나는 오른손을 드는 것으로 보입니다. 즉, 거울 속에 비치는 모습은 왼쪽과 오른쪽이 뒤집힌 대칭이동의 결과입니다. 우리가 스마트폰 등을 이용해 혼자 사진을 찍을 때도 좌우를 혼동하거나 앞뒤 거리를 잘 못 맞추는 것 등이 이런 이유에서 흔히 발생하는 현상이지요.

사실 거울은 좌우 방향으로 뒤집히는 것이 아니고 앞뒤 방향으로 뒤집히게 됩니다. 내가 거울을 보고 있을 때, 거울 속의 나는 나와 반대 방향을 바라보고 있기 때문에 우리가 바라볼 때는 좌우가 반대로 뒤집힌 것처럼 보이게 됩니다. 사람들이 흔히 거울이 ‘좌우가 바뀐다’라고 착각하는 이유는 앞뒤를 먼저 기준으로 잡은 다음 좌우를 판단하는 사고방식 때문이라고 합니다.

거울 표면에 빛을 비추면 거울 표면에서 반사를 합니다. 이때 들어가는 빛과 거울 표면에 수직인 선이 이루는 각을 입사각이라하고 반사한 빛과 거울 표면에 수직인 선과 이루는 각을 반사각이라고 합니다. 입사각과 반사각의 크기는 항상 같은데 이를 반사의 법칙이라 합니다. ‘그림2’같이 거울에 비친 상을 볼 때 물체에서 반사한 빛이 거울을 향해 여러 방향으로 입사한 빛이 거울 면에서 각각 입사한 각과 같은 각으로 반사되어 여러 방향으로 나아갑니다. 이같이 반사된 빛의 일부 중 우리의 눈으로 들어오지요. 그런데 우리 눈에 보이게 되는 것은 반사 후 직진하는 빛이므로 우리 눈에는 거울 안쪽에서 직진하여 나오는 것처럼 보입니다. 따라서 실물과 같은 크기의 상이 거울 안쪽으로 같은 거리만큼 떨어진 곳에 나타나고 거울에 비친 상은 좌우가 바뀌어 보입니다.

○ 선·면·회전… 다양한 대칭의 세계

‘그림3’으로 선대칭과 면대칭을 조금 더 수학적으로 알아볼까요. 평면 위의 직선이 있다고 할 때, 평면 위의 점 P에서 직선에 내린 수선의 발을 M이라 합시다. M을 지난 수선을 연장하고 점 P‘를 그리면 선분 PM과 선분 P’M의 길이가 같을 때 점 P‘은 직선에 대한 대칭점이라고 합니다. 이때 점 P는 직선에 대해서 점 P’의 대칭점이기도 하기에 두 점은 직선에 대해 선대칭이라고 합니다. 점 P를 직선에 대한 대칭점 P‘로 옮길 때 이를 대칭이동이라 합니다. 이때 직선은 대칭축이 됩니다. 이를 확장해 공간에서의 평면 S에 대하여 같은 방식으로 공간상의 점 P에서 평면 S에 내린 수선의 발을 M이라 합시다. M을 지난 수선을 연장하고 점 P’를 그리면 선분 PM과 선분 P‘M의 길이가 같을 때 점 P와 P’은 평면 S에 대하여 면대칭이라고 합니다. 이때 평면 S는 대칭면이 됩니다. 앞서 설명한 거울상은 원래의 도형과 면대칭의 관계에 있으면 대칭면은 거울 표면이 되는 것입니다.

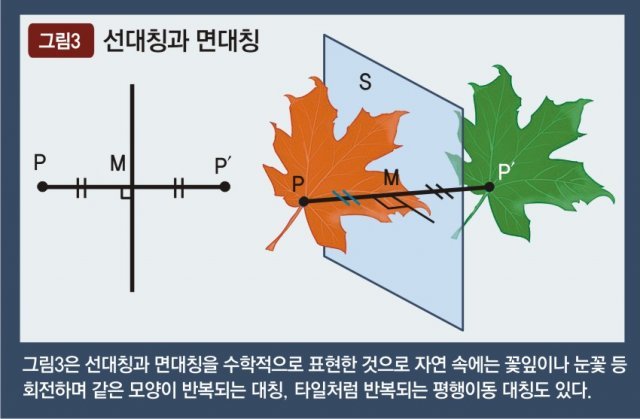
자연과 우리 주변에는 네 잎의 꽃잎처럼 90도를 회전하면 모양이 되풀이되거나 눈의 결정처럼 60도 회전을 하면 다시 모양이 같아지는 회전대칭이나, 타일처럼 일정한 공간마다 되풀이되는 평행이동 대칭도 있습니다.

단계적 일상 회복에 맞춰 코로나19로 제한되었던 나들이를 조심스레 시작해봅니다. 방역은 철저히 하되 맑은 공기와 풍광을 몸과 마음으로 즐기면서도 대칭의 눈으로 주변을 관찰하며 생각으로도 즐기는 가을 나들이가 되기 바랍니다. 특히 조화로움의 다양한 대칭을 발견한다면 사진으로 남겨도 좋을 것입니다.