[신문과 놀자!/눈이 커지는 수학]낮이 가장 짧아지는 ‘동지’… 기하학 원리로 알아볼까요?

올해 12월 22일은 일년 중 가장 낮이 짧은 날이자 밤이 가장 긴 날입니다. 바로 24절기의 22번째 절기인 동지입니다. 24절기는 지구가 태양의 둘레를 도는 길인 황도를 따라 15도(15도×24=360도)씩 돌 때마다 기상과 동식물의 변화 등을 나타내어 명칭을 붙인 것입니다.

○ 계절마다 밤낮의 길이가 다른 이유

그림1

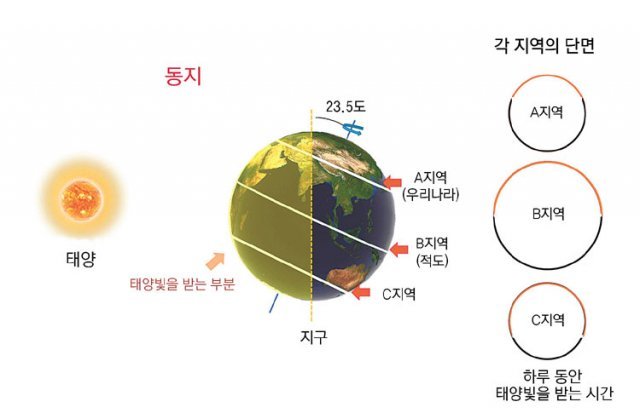
지구가 23.5도 기울어져 있기 때문에 태양의 고도가 가장 높아지는 경우와 가장 낮아지는 경우가 생깁니다. 이것이 동지와 하지를 결정하는 요인이지요. 동지에 우리나라는 태양에 공전할 때 지구의 자전축이 그림과 같이 위치합니다. 이 시기에 우리나라를 포함한 지구의 A, B, C 지역의 위치를 자전축에 수직인 선으로 나타내고 그 단면을 그려보면, 그림의 오른쪽과 같이 각 원둘레에서 하루 동안 태양 빛을 받는 시간의 비율이 나타납니다.(그림1)

이처럼 태양빛을 받는 시간은 각 지역마다 다릅니다. 해가 늦게 떠서 일찍 지는 곳도 있고, 일찍 떠서 늦게 지는 곳도 있겠지요. 만약 지구의 자전축이 기울어져 있지 않다고 생각해봅시다. 그러면 각 지역의 낮과 밤의 길이는 어떻게 될까요. 아마 낮과 밤의 길이는 어느 지역이든 동일할 것입니다.

여기에서 또 하나 생각할 것은 지구가 공전을 한다는 것입니다. 겨울 동지의 경우는 그림과 같이 태양 빛이 자전축 왼쪽에서 들어오지만, 여름에는 이와 반대 방향으로 태양빛이 자전축 오른쪽으로 들어옵니다. 그러면 낮과 길이가 바뀌어 C지역이 낮이 가장 짧고 A지역이 낮이 길어지는 것이지요. 여전히 적도지방에서는 동지와 하지라는 개념이 생기지 않지만 자전축에 수직인 선을 극지방으로 이동하여 살펴보면 계속 해가 뜨거나 아예 뜨지 않은 경우가 있을 수 있음을 알 수 있습니다.

○ 빛과 그림자, 그리고 수학

어린 시절 조명 아래서 그림자놀이를 하거나 동네에서 그림자밟기 놀이를 한 기억도 있을 겁니다. 인류는 이러한 그림자의 성질을 이용하여 시계도 만들고 그림자 길이를 이용해 건축물의 높이, 지구의 둘레를 구하기도 했습니다.

이것은 태양 덕분에 가능했습니다. 태양 광선은 평행광선이기 때문에 그림자에 ‘합동’이나 ‘닮음’이라는 수학이 숨어 있습니다. 건물의 높이를 알고 싶을 때, 이를 잴 수 있는 자가 없는 것은 물론이고 또 이미 입체 형태의 건물의 높이를 재는 것도 쉽지는 않습니다. 그러나 그림자의 길이를 이용하면 간단히 해결됩니다. 우선 곧은 막대기를 하나 준비해 그 길이를 잽니다. 그다음에는 막대기를 땅바닥에 곧바로 세우지요. 막대기의 그림자 길이를 재고, 같은 시각에 건물의 그림자의 길이도 잽니다. 건물의 길이를 잴 수는 없지만 건물의 그림자 길이는 잴 수 있으니까요.

그림2

예를 들어 막대의 길이는 50cm, 그림자의 길이는 20cm일 때, 같은 시각 어느 건물의 중심부부터 그림자 끝부분까지의 길이를 재었더니 222m가 되었다면 건물의 높이와 그림자의 길이, 막대의 길이와 그림자의 길이 사이에 비례식 ‘20:50=222:χ’가 성립합니다.(그림2) 이때 ‘χ’를 구하면 건물의 높이는 555m입니다. 이것은 평행하게 비추는 태양 빛에 의해 생긴 그림자와 물체가 이루는 직각삼각형이 서로 닮음이 되기 때문이지요.

그림3

고대 그리스 시대에 살던 에라토스테네스는 닮음을 이용하여 지구의 둘레를 재었다고 합니다. 당시 사람들도 북극성의 고도가 위치에 따라 다르다는 사실로부터 지구가 둥글다고 생각했다고 합니다. 에라토스테네스는 여름 하지에 그림자를 통해 태양이 하루 중 가장 높은 고도가 90도라고 판단되는 이집트의 한 장소와 그로부터 북쪽으로 지금의 거리로는 약 925km 떨어졌다고 추정되는 지점에서 같은 시각에 태양 빛이 7.2도 기울어져 들어온다는 사실을 알았습니다. 호의 길이는 중심각의 크기에 비례하므로 ‘(지구의 둘레):925km=360도:7.2도’라는 비례식을 만들 수 있습니다.(그림3)

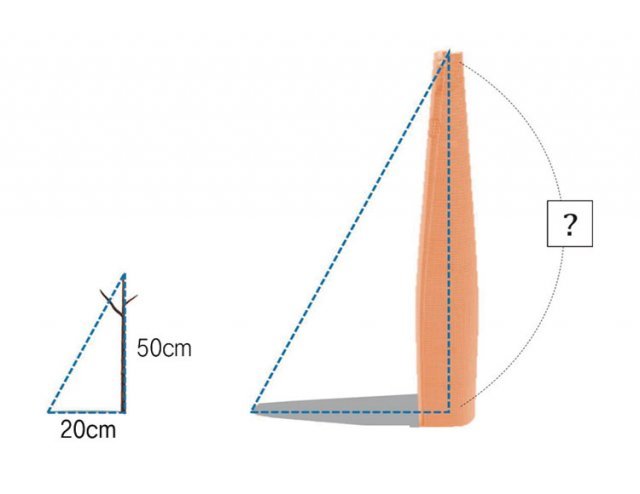
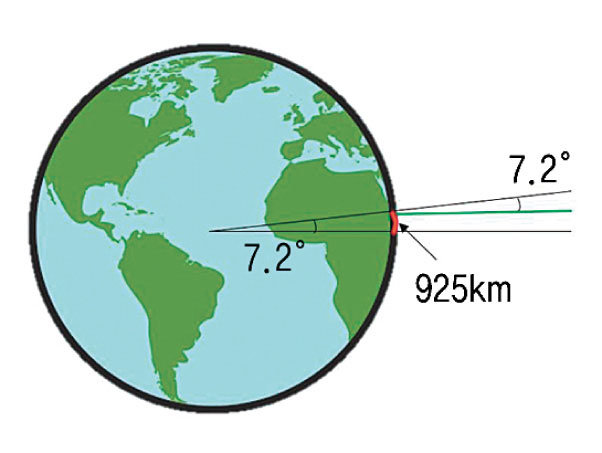
이를 통해 지구의 둘레를 구해냈고 오늘날 거리 단위로 환산하면 (360÷72)×925=46,250(km)이 됩니다. 오늘날 알아낸 실제 지구의 둘레는 40,192km로 차이는 있습니다. 오차가 있긴 하지만 커다란 지구의 둘레를 훌륭하게 구해낸 예입니다.

○ 그림자를 탐구하는 수학, 정사영

태양 빛은 지구의 자전으로 뜨고 집니다. 빛이 물체를 사이에 두고 바닥 면과 다양한 각도로 들어올 때 생기는 그림자는 같은 물체라도 크기나 모양이 다양하게 변합니다. 그러나 또 변하지 않는 성질도 있습니다. 직선인 빛과 수직인 면에 의해 생기는 그림자의 경우는 공통적인 특성이 있습니다.

빛이 그림자가 생기는 면에 수직으로 비출 때와 같이 도형의 각 점에서 한 평면에 내린 수선의 발이 그리는 도형을 정사영이라고 합니다. 이 경우 본래 도형인 선분의 길이와 정사영의 길이는 직각삼각형의 한 각에 대한 빗변과 밑변의 비의 관계를 그대로 가지게 됩니다.

그림4

태양이 움직이는 동안 그림자의 위치도 크기도 바뀝니다. 정사영을 역으로 이용하면 그림자의 넓이를 구할 수 있습니다. 다시 말해 태양 빛에 수직인 물체의 면을 도형 A′으로 이해하고 그림자를 도형 A로 보면, 그림자 도형 A의 넓이는 관계식 A×cosθ=A′에서 구할 수 있습니다.(그림4)

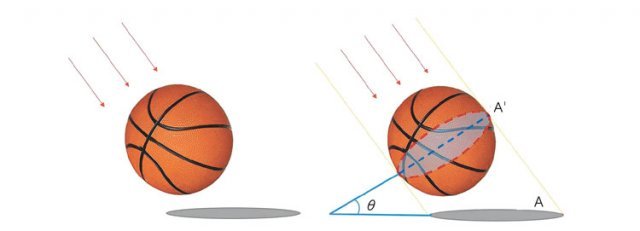
동짓날 팥죽을 먹으며 다양한 물체의 그림자의 변화도 관찰해보세요. 또 주변의 다양한 건물의 높이를 그림자로 구해보세요. 지구와 태양에 숨어 있는 수학이 느껴질 것입니다.