[황규인의 잡학사전] MLB 스카우트는 왜 20~80점만 쓸까

동아일보
입력 2017년 9월 20일 13시 41분

황규인 기자

코멘트: 개

좋아요: 개

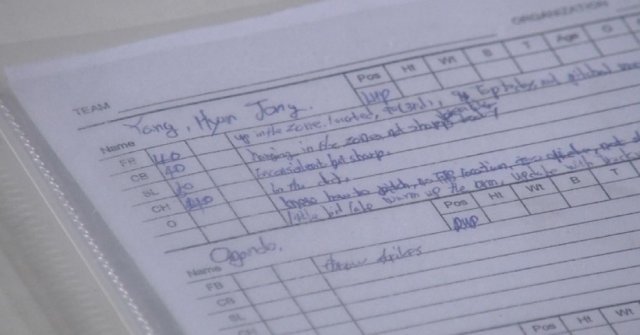
한 메이저리그 스카우트가 KIA 투수 양현종(29)에 대해 작성한 스카우팅 리포트(사진)가 19일 프로야구 TV 중계화면에 잡혔습니다. 빠른 공(FB) 40, 커브(CB) 40, 슬라이더 50, 체인지업 40이라고 평가했네요. 이렇게 점수를 매기면 흔히 0~100점 사이라고 생각하기 쉽지만, 메이저리그 스카우트는 20~80점 범위만 씁니다. 왜 그럴까요?

정답은 ‘정규분포’ 때문입니다. 네, 수학 시간에 배우는 그 정규분포 맞습니다. 평균을 50점, 표준편차를 10점으로 정규분포 그래프를 그리면 아래 그림처럼 나타납니다.

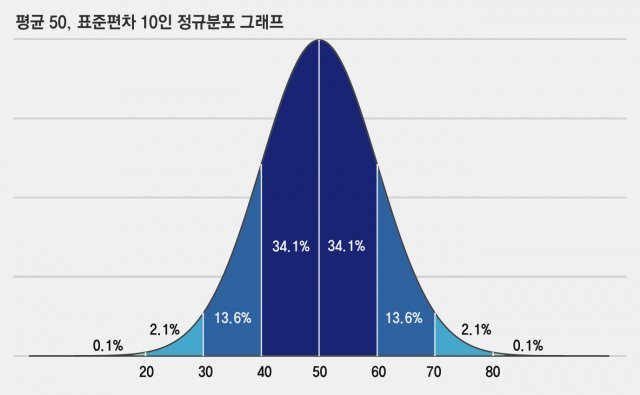
이때 비율은 해당 구역에 전체 표본 중 몇 %가 들어있는지를 나타냅니다. 20 아래와 80 너머에는 각 0.1%밖에 들어있지 않습니다. 그러니까 20~80점만 써도 전체 표본 중 99.8%를 커버할 수 있는 거죠. 스카우트 사이에선 20~80점을 아래와 같은 뜻으로 씁니다.

80: 아주 뛰어남(Outstanding)
70: 뛰어남(Well-above-average)
60: 평균 이상(Above-average)
50: 메이저리그 평균(Major league average)
40: 평균 이하(Below-average)
30: 부족함(Well-below-average)
20: 매우 부족함(Poor)

팀에 따라서는 이 숫자를 10으로 나눠 2~8점을 기준으로 삼는 팀도 있습니다. 그래도 의미는 똑같습니다. 20~80점은 스카우트 사이에서 ‘링구아 프랑카(공용어)’입니다.

여기서 잠깐. 지금부터 길고 지루하게 역사적 배경과 20~80점이 야구에서 어떤 의미가 있는지 설명할 예정입니다. 이런 내용은 알고 싶지 않다고 생각하시는 분은 1)아래 추천을 눌러주시고 다른 기사를 읽으시거나 2)천천히 스크롤을 아래로 내리시다가 마음에 드는 그림이 나오는 부분부터 읽어주시면 감사하겠습니다.

●누가 먼저 썼을까

아, 계속 읽기로 하셨군요. 정말 감사합니다. 오늘은 행운이 가득한 하루가 될 겁니다.

물론 메이저리그 스카우트들이 처음부터 이런 기준을 썼던 건 아닙니다. 처음에는 당연히 ‘말’로 리포트를 적었습니다. 선수 스카우트라는 건 원래 주관이 많이 개입할 수밖에 없는 법. 그냥 말로 하면 상대가 무슨 이야기를 하는지 알아차리기가 더욱 어려울 겁니다. 그다음에는 평균을 A로 두고 평균보다 좋으면 A+, A++, A+++…, 나쁘면 A0, A00, A000…처럼 등급을 매기는 방식을 썼지만 헷갈리는 마찬가지였습니다. 이럴 때는 확실히 숫자가 편합니다.

야구 역사학자들이 스카우트에 처음 숫자를 도입한 인물로 제일 많이 거론하는 건 브랜치 리키 전 브루클린(현 LA) 다저스 단장(1881~1965)입니다. 리키 단장은 마이너리그에서 메이저리그로 이어지는 현재 팜(farm·선수 육성) 시스템을 고안한 인물입니다. 타고난 능력을 뜻하는 ‘툴(tool·도구)’ 역시 리키 단장이 처음 사용한 개념입니다.

리키 단장(오른쪽)은 메이저리그 인종 차별에 종지부를 찍은 인물로도 유명합니다. 왼쪽은 20세기 들어 아프리카계 미국인으로 처음 메이저리거가 된 재키 로빈슨(1919~72).

▶ML 흑인선수 19세기에도 있었다

단, 리키 단장은 0~60점 범위를 썼습니다. 리키 단장 제자로 역시 다저스 살림을 맡았던 알 캄파나이스 단장(1916~98)은 60~80점 범위를 선택했습니다. 그는 “학교 선생님처럼 생각했던 거다. 70점을 통과 기준으로 삼고 80점 이상이면 우등생, 60점 아래면 낙제생이라는 생각으로 접근했던 것”이라고 설명했습니다.

그러다가 1974년 메이저리그 17개 구단이 각출해 스카우트 사무국(MLB Scouting Bureau)을 만들면서 20~80 시스템이 자리를 잡게 되죠. 이 사무국 초대 수장을 맡았던 짐 윌슨 전 밀워키 단장(1922~86) 아이디어였습니다.

당시 부국장을 맡았던 돈 프리스 전 볼티모어 스카우트(90)는 “윌슨 국장과 ‘어떻게 하면 표준화된 평가 시스템을 만들 수 있을까 브레인스토밍을 하다가 이 개념을 떠올렸다. 세월이 흘러서 구체적인 내용은 기억이 나지 않는다. 윌슨 국장이 먼저 세상을 떠나 물어볼 사람도 없다. 하늘에 가서 꼭 물어보겠다”며 웃었습니다.

●도대체 정규분포로 어떻게 평가할까?

물론 그렇다고 스카우트가 ’저 선수 커브는 메이저리그 평균보다 1 표준편차만큼 뛰어나니 60점을 줘야겠다‘고 평가하는 건 아닙니다. 오히려 많은 평가가 쌓이면 쌓일수록 정규분포를 향해 가는 방식입니다. 사실 자연에 존재하는 모든 현상은 시행 횟수를 늘리면 점점 정규분포에 가까운 모양이 됩니다.

예를 들어 이론적으로 동전을 100번 던지면 앞면은 50번이 나와야 합니다. 단, 실제로 동전을 100번을 던졌다고 해서 꼭 50번이 나오라는 법은 없습니다. 실제로 앞면이 나오는 확률은 아래 그림처럼 분포합니다. 어떻습니까? 정규분포를 닮았죠?

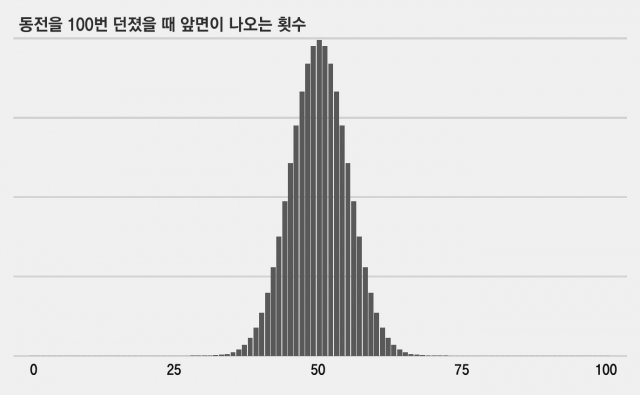
여기서 중요한 건 우리가 동전을 던지면 앞면이 나올 확률이 2분의 1이라는 걸 알고 있다는 점입니다. 마찬가지로 메이저리그 스카우트가 되려면 50점 그러니까 평균이 뭔지 정확히 알고 있어야 합니다. 스카우트 사무국은 1989년부터 12일짜리 스카우트 양성 프로그램을 진행하면서 교육 과정 상당 부분을 이 50점을 보는 눈 기르기에 할당하고 있습니다.

또 어떤 경우에 각 점수를 주는지 세세한 내용도 정해두고 있습니다. 가장 일반적인 교육 방식은 이미 스타가 된 선수가 예전에 어떤 점수를 받았는지 되돌려보는 것. 또 스카우트 지망생은 유망주가 있다면 현재 스타인 어떤 선수와 비교해 보라는 지시도 받게 됩니다.

어떤 툴은 아예 객관적인 범위를 정해 놓고 모든 스카우트가 공통으로 사용하기도 합니다. 아래 표는 스카우트닷컴에서 찾은 예시입니다.

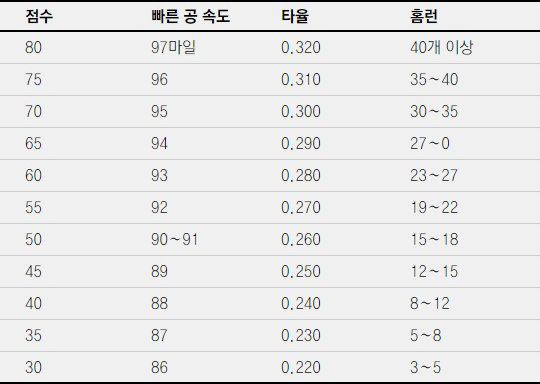
이 표에는 20이 없습니다. 스카우트닷컴에서는 “어떤 항목이든 20을 받을 정도면 스카우트는 관심이 없다고 봐야 한다. 20을 쓰는 건 뚱뚱한 타자가 아주 발이 느릴 때 정도뿐”이라고 설명하고 있습니다.

스카우트가 야수를 평가하는 항목은 그 유명한 파이브(5)툴. 이 다섯 가지는 △타격 능력(Hitting Ability) △파워(Power) △스피드(Running Speed) △어깨(Arm Strength) △수비력(Fielding)입니다. 투수는 위에 나온 것처럼 빠른 공, 커브, 슬라이더 그리고 나머지 주요 구종에 대해 20~80점으로 점수를 매기게 됩니다.

●정규분포 또 언제 쓸까

정규분포는 야구 선수 스카우트 때처럼 평가 때 자주 씁니다. 대학수학능력시험 등에서 표준점수를 구할 때 쓰는 것 역시 정규분포입니다. ’등급제 수능‘에서는 성적이 상위 몇 %에 속하는지를 구하고(백분위) 이를 평균 50, 표준편차를 20으로 하는 정규분포에 대응해 표준점수를 구했습니다. 이 표준점수가 어떤 구간에 속하는지에 따라 등급을 결정했죠.

정규분포를 이야기할 때 빼놓을 수 없는 사람이 독일 출신 수학자 카를 프리드리히 가우스(1777~1855)입니다. 가우스는 소행성을 찾다가 이 분포를 발견했습니다. 그래서 정규분포를 ’가우스 분포‘라고 부르기도 합니다. 혹시 포토샵 같은 프로그램으로 그래픽 작업을 하시다가 이미지를 흐리게 하는 ’가우시안(Gaussian) 필터‘ 같은 용어를 보신 적 있으신가요? 네, 이 필터를 가능하게 하는 원리 역시 정규분포입니다.