[신문과 놀자!/눈이 커지는 수학]동그라미 대신 정육각형… 우주망원경에 숨겨진 다양한 수학 원리

18개 육각형으로 반사거울 나눠 발사… 원보다 정육각형이 잘 들어맞고
대칭적 특성 이용 땐 제작도 수월, 150만 ㎞ 떨어진 L2 궤도서 태양 공전
지구와 일직선 유지하며 망원경 보호

18세기 수학자 라그랑주는 세 개의 천체가 궤도를 돌며 안정적인 위치를 유지할 수 있는 ‘라그랑주점’을 발견했다. NASA 제공

지난해 12월 25일 발사를 성공적으로 마친 차세대 우주망원경 ‘제임스 웹 우주망원경(JWST)’이 지구로부터 150만 km 떨어진 도착 지점에서 최근 1월 31일(현지 시간) 전원공급 장치를 가동하며 본격적인 우주 관측에 돌입했다는 소식이 전해졌습니다.

우주로 날아간 것 중 가장 큰 너비의 거울을 자랑하며 소행성, 외계행성, 먼지, 블랙홀 및 먼 은하 등 별의 탄생이나 우주 생성과 진화를 조사할 예정입니다. 제임스 웹 우주망원경이 최초로 관측한 선명한 천체 이미지는 6월 말 또는 7월 초에 공개될 예정이라고 합니다.

서영: 지난해 발사된 제임스 웹 우주망원경의 육각형 금빛 거울이 너무 인상적이었어요.

엄마: 우리가 보통 생각하는 망원경과 너무 달랐지? 보통은 원형 렌즈인데 말이다. 우주망원경이나 로켓 등 형태와 발사에서부터 운항까지 항공 분야에서도 수학이 중요한 역할을 한단다.

○18개의 육각형 거울로 보는 우주

제임스 웹 망원경은 18개의 육각형 거울로 분할되도록 설계됐다. NASA 제공

제임스 웹 우주망원경은 1990년부터 임무를 수행 중인 허블 우주망원경보다 성능이 개선된 망원경으로 베릴륨을 주 소재로 그 질량이 허블 우주망원경의 절반 수준인 6.5t입니다. 주 반사 거울의 지름은 6.5m로 2.4m인 허블 우주망원경의 2.5배에 달해 뛰어난 관측 성능이 기대되고 있습니다.

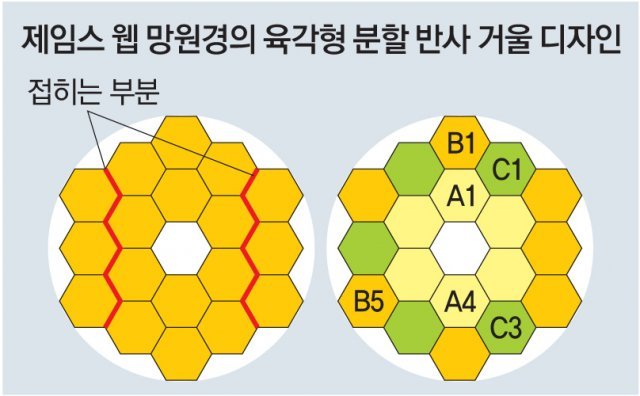
그런데 이 망원경의 주 반사 거울은 한 장이 아니라 18개의 육각형 조각으로 분할돼 있지요. 또 전체가 마치 거대한 육각형처럼 보이기도 합니다. 이 반사 거울 조각들은 발사 전에는 로켓 안에 접혀져 있다가 망원경이 발사된 후 우주에서 펼쳐지도록 설계됐습니다.

먼저 주 반사 거울 전체의 정육각형처럼 보이는 모양은 사실 거의 원형에 가깝습니다. 망원경의 구조상 검출기의 가장 조밀한 영역에 빛을 집중시키기 때문에 전체 거울 모양은 원형이 바람직합니다.

그렇다면 왜 거울을 정육각형의 조각으로 분할했을까요? 우선 커다란 원형 거울을 우주로 그대로 보내는 데는 어려움이 있으니 면을 분할해야겠죠. 이때 면을 채우는 데 있어 비율이 가장 높은 도형인 정육각형을 선택한 것입니다. 면을 채우는 비율이 높다는 것은 분할된 부분이 틈이 없이 함께 잘 들어맞는다는 것을 의미합니다. 분할된 모형이 원형이라면 그 사이에 간격이 생기겠지요. 그리고 이를 삼각형으로 한다면 지금보다 많은 개수의 분할이 필요할 것입니다. 현재 지상 천문대용으로 제작되고 있는 대부분의 망원경 거울은 육각형 분할 디자인을 사용합니다. 수십 번 복제된 작은 너비의 육각형 하나는 큰 거울 하나보다 훨씬 만들기가 쉽기 때문입니다.

정육각형의 또 다른 특성은 60도 회전하면 패턴이 처음 시작한 것과 동일하게 보인다는 것입니다. 이러한 성질을 대칭이라고 합니다. 중심에서 가장 가까운 타일 6면 중 하나에 A라는 이름을 붙인다고 가정합니다. 이 육각형을 60도씩 회전하면 A면이 다시 자기 자리로 오는 데 정확히 6번의 이동이 필요합니다. 제임스 웹 우주 망원경은 이러한 대칭 특성을 살려 거울 중심에서 특정 거리에 위치한 타일을 정확히 동일한 광학 특성의 거울로 조립했습니다. 예를 들어 ‘제임스 웹 망원경의 육각형 분할 반사 거울 디자인’의 오른쪽 그림에서 A라고 이름 붙여진 6개 타일의 내부 링은 각 링의 다른 타일과 60도 회전해 동일한 성질을 갖는 타일을 가지고 있고 B, C로 표현된 타일도 시계 방향으로 번호를 붙이면 6개 모두 동일한 거울입니다.

분할된 각 타일 자체도 거울입니다. 18개의 거울 타일이 함께 작동해 하나의 큰 거울을 형성한 뒤 희미한 별빛을 수집합니다. 망원경 거울에서 중요한 것은 표면적입니다. 거울의 표면적이 넓을수록 더 많은 빛을 모을 수 있습니다. 희미한 별과 은하를 자세히 연구할 수 있을 만큼 밝게 보이게 하려면 모아진 면적이 큰 거울이 필요합니다.

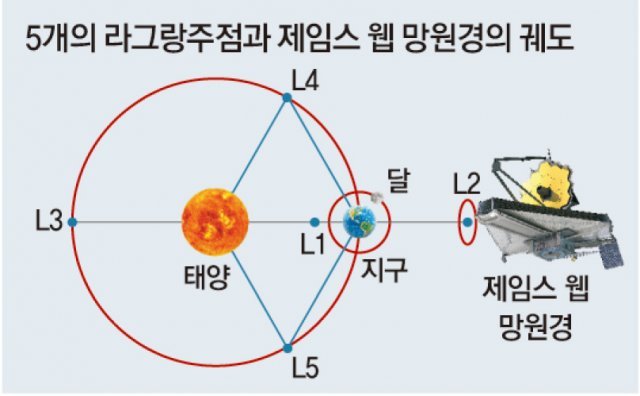
○300년 전 수학으로 찾아낸 우주망원경 궤도

우주로 발사된 제임스 웹 우주망원경은 L2 위치에 머무를 예정이다. NASA 제공

제임스 웹 우주망원경은 허블 우주망원경처럼 지구 주위를 돌지 않습니다. 지구에서 150만 km 떨어진 두 번째 라그랑주점 또는 ‘L2’ 궤도에서 태양을 돕니다. 이 궤도를 돌면 망원경이 태양 주위를 이동할 때 지구와 일직선을 유지할 수 있습니다. 이를 통해 위성의 대형 가림막이 빛과 열로부터 망원경을 보호할 수 있습니다.

18세기 수학자 조제프 루이 라그랑주는 세 개의 천체가 서로 궤도를 도는 동시에 서로에 대해 동일한 위치를 유지할 수 있는 안정적인 위치를 찾는 문제로 불리는 삼체 문제를 수학적으로 해결해 5개의 지점을 찾았습니다. 이 다섯 지점 중 하나에 위치한 우주선과 같은 물체는 태양과 지구 등 다른 물체에 비해 제자리에 머무르기가 쉽다고 합니다.

이 지점은 발견자를 기리기 위해 5개의 라그랑주점이라 하고 각각 L1, L2, …, L5로 나타냅니다. L1, L2, L3 점은 모두 일직선상에 있으며 L4와 L5는 정삼각형 점에 있습니다. 라그랑주점에서 두 개의 큰 물체 중력은 작은 물체가 함께 움직이는 데 필요한 구심력과 정확히 같습니다. L4와 L5는 그곳에 있는 물체가 도움 없이 L4와 L5를 공전한다는 점에서 안정적이지만 L1, L2 및 L3 점 주변의 물체는 예를 들어 작은 주기적 로켓 추력을 사용해 위치를 유지하지 않는 한 태양 주위의 자체 궤도로 천천히 표류하는 등 ‘준안정적’이라 합니다. L2 궤도는 준안정 두 번째 라그랑주점을 중심으로 한 타원 궤도입니다.

제임스 웹 망원경 프로젝트는 1990년대 후반부터 허블망원경보다 ‘더 크게, 더 먼 곳에’ 새로운 망원경을 배치할 계획을 실현하려 노력해 온 결과입니다. ‘더 크게’는 대칭인 육각형 도형에서 찾고, ‘더 먼 곳에’는 300년 전 수학자의 연구 결과에서 찾았던 것이지요. 지금 우리의 작은 노력이 언젠가 인류의 탐구 의지를 실현시킬 실마리가 될지도 모릅니다.